Biomechanical Analysis of Left Ventricle Considering Myocardial Infarction and Regenerative Therapy Using Dynamic Finite Element Method
Article Information
Shahrul Hisyam Marwan1,2 and Mitsugu Todo1,3*
1Interdisciplinary Graduate School of Engineering Sciences, Kyushu University, Fukuoka, Japan.
2College of Engineering, University Technology MARA, Terengganu, Malaysia.
3Research Institute for Applied Mechanics, Kyushu University, Fukuoka, Japan.
*Corresponding Author: Mitsugu Todo, Associate Professor Research Institute for Applied Mechanics, Kyushu University
Received: 08 May 2021; Accepted: 18 May 2021; Published: 21 May 2021
Citation:
Shahrul Hisyam Marwan, Mitsugu Todo, Biomechanical Analysis of Left Ventricle Considering Myocardial Infarction and Regenerative Therapy Using Dynamic Finite Element Method. Journal of Biotechnology and Biomedicine 4 (2021): 10-25.
View / Download Pdf Share at FacebookAbstract
It is well known that myocardial infarction (MI) greatly degrades the pulsation function of the heart. Such MI may gradually grow in size and harden as ischemic necrosis proceeds, resulting in further degradation of its pulsation behavior. However, regenerative therapy has successfully been used in the medical treatment of MI, specifically the use of cell sheet technology. In this procedure, thin sheets of biomechanical effects of regenerative therapy on the LV with MI. A simple 3D finite element model of a LV was developed and dynamic FEA with a cardiac mechanics theory was conducted to simulate the time-dependent cyclic deformation behavior. It was found that increasing size and stiffness of the MI dramatically reduced both the maximum displacement of beating mechanical behavior. It was also determined that the cardiac cell sheet regenerative therapy can effectively restore the pulsation function.
Keywords
Myocardial infarction; Human heart; Dynamic finite element method; Cardiac mechanics
Myocardial infarction articles Myocardial infarction Research articles Myocardial infarction review articles Myocardial infarction PubMed articles Myocardial infarction PubMed Central articles Myocardial infarction 2023 articles Myocardial infarction 2024 articles Myocardial infarction Scopus articles Myocardial infarction impact factor journals Myocardial infarction Scopus journals Myocardial infarction PubMed journals Myocardial infarction medical journals Myocardial infarction free journals Myocardial infarction best journals Myocardial infarction top journals Myocardial infarction free medical journals Myocardial infarction famous journals Myocardial infarction Google Scholar indexed journals Human heart articles Human heart Research articles Human heart review articles Human heart PubMed articles Human heart PubMed Central articles Human heart 2023 articles Human heart 2024 articles Human heart Scopus articles Human heart impact factor journals Human heart Scopus journals Human heart PubMed journals Human heart medical journals Human heart free journals Human heart best journals Human heart top journals Human heart free medical journals Human heart famous journals Human heart Google Scholar indexed journals Dynamic finite element method articles Dynamic finite element method Research articles Dynamic finite element method review articles Dynamic finite element method PubMed articles Dynamic finite element method PubMed Central articles Dynamic finite element method 2023 articles Dynamic finite element method 2024 articles Dynamic finite element method Scopus articles Dynamic finite element method impact factor journals Dynamic finite element method Scopus journals Dynamic finite element method PubMed journals Dynamic finite element method medical journals Dynamic finite element method free journals Dynamic finite element method best journals Dynamic finite element method top journals Dynamic finite element method free medical journals Dynamic finite element method famous journals Dynamic finite element method Google Scholar indexed journals Cardiac mechanics articles Cardiac mechanics Research articles Cardiac mechanics review articles Cardiac mechanics PubMed articles Cardiac mechanics PubMed Central articles Cardiac mechanics 2023 articles Cardiac mechanics 2024 articles Cardiac mechanics Scopus articles Cardiac mechanics impact factor journals Cardiac mechanics Scopus journals Cardiac mechanics PubMed journals Cardiac mechanics medical journals Cardiac mechanics free journals Cardiac mechanics best journals Cardiac mechanics top journals Cardiac mechanics free medical journals Cardiac mechanics famous journals Cardiac mechanics Google Scholar indexed journals circulatory articles circulatory Research articles circulatory review articles circulatory PubMed articles circulatory PubMed Central articles circulatory 2023 articles circulatory 2024 articles circulatory Scopus articles circulatory impact factor journals circulatory Scopus journals circulatory PubMed journals circulatory medical journals circulatory free journals circulatory best journals circulatory top journals circulatory free medical journals circulatory famous journals circulatory Google Scholar indexed journals mortality and morbidity articles mortality and morbidity Research articles mortality and morbidity review articles mortality and morbidity PubMed articles mortality and morbidity PubMed Central articles mortality and morbidity 2023 articles mortality and morbidity 2024 articles mortality and morbidity Scopus articles mortality and morbidity impact factor journals mortality and morbidity Scopus journals mortality and morbidity PubMed journals mortality and morbidity medical journals mortality and morbidity free journals mortality and morbidity best journals mortality and morbidity top journals mortality and morbidity free medical journals mortality and morbidity famous journals mortality and morbidity Google Scholar indexed journals treatments articles treatments Research articles treatments review articles treatments PubMed articles treatments PubMed Central articles treatments 2023 articles treatments 2024 articles treatments Scopus articles treatments impact factor journals treatments Scopus journals treatments PubMed journals treatments medical journals treatments free journals treatments best journals treatments top journals treatments free medical journals treatments famous journals treatments Google Scholar indexed journals Biomechanical Analysis articles Biomechanical Analysis Research articles Biomechanical Analysis review articles Biomechanical Analysis PubMed articles Biomechanical Analysis PubMed Central articles Biomechanical Analysis 2023 articles Biomechanical Analysis 2024 articles Biomechanical Analysis Scopus articles Biomechanical Analysis impact factor journals Biomechanical Analysis Scopus journals Biomechanical Analysis PubMed journals Biomechanical Analysis medical journals Biomechanical Analysis free journals Biomechanical Analysis best journals Biomechanical Analysis top journals Biomechanical Analysis free medical journals Biomechanical Analysis famous journals Biomechanical Analysis Google Scholar indexed journals Left Ventricle articles Left Ventricle Research articles Left Ventricle review articles Left Ventricle PubMed articles Left Ventricle PubMed Central articles Left Ventricle 2023 articles Left Ventricle 2024 articles Left Ventricle Scopus articles Left Ventricle impact factor journals Left Ventricle Scopus journals Left Ventricle PubMed journals Left Ventricle medical journals Left Ventricle free journals Left Ventricle best journals Left Ventricle top journals Left Ventricle free medical journals Left Ventricle famous journals Left Ventricle Google Scholar indexed journals Regenerative Therapy articles Regenerative Therapy Research articles Regenerative Therapy review articles Regenerative Therapy PubMed articles Regenerative Therapy PubMed Central articles Regenerative Therapy 2023 articles Regenerative Therapy 2024 articles Regenerative Therapy Scopus articles Regenerative Therapy impact factor journals Regenerative Therapy Scopus journals Regenerative Therapy PubMed journals Regenerative Therapy medical journals Regenerative Therapy free journals Regenerative Therapy best journals Regenerative Therapy top journals Regenerative Therapy free medical journals Regenerative Therapy famous journals Regenerative Therapy Google Scholar indexed journals
Article Details
1. Introduction
The primary function of heart is to distribute blood through the circulatory system for the maintenance of life. Therefore, if the heart has a severe problem, such as myocardial infarction (MI), the life of the patient could be in severe danger. MI occurs when blood flow at a coronary artery dramatically decreases due to arteriosclerosis and hence blood supply to the heart muscle is significantly reduced, resulting in severe damage to the myocardium [1,2]. If MI occurs, it can deteriorate the cardiac function and increase the risk of heart failure. Worldwide, MI is said to be one of the most significant causes of mortality and morbidity [3-6], for instance there are about 1.5 million annual deaths in the United States associated with MI [7]. The mortality of MI has decreased significantly through the development of revascularization therapies, such as coronary artery bypass grafting, thrombolytic agents, and percutaneous coronary intervention [8]. Nevertheless, the occurrence of heart failure due to MI has not essentially dropped [9]. An inadequate blood supply to the heart may result in the death of normal heart muscle tissue through necrosis, apoptosis, and/or autophagy and the subsequent development of scar tissue decreases the capability of heart contraction [10,11]. Since adult cardiomyocytes have limited regenerative capacity, the damage can be permanent, which can result in heart failure and death [12-14].
Over the past two decades, complex medical treatments have been developed for cardiac transplantation; however, donor shortage is a major challenge that limits this approach. In addition, immunosuppressive drug therapy is required to be taken by the transplant patients after surgery to reduce the risk of transplant rejection, which comes with a whole host of negative side-effects [14]. To overcome these problems, regenerative medicine of the heart has extensively been investigated, and some clinical techniques have effectively been developed.
Very recently, an effective regenerative medicine technique for damaged hearts has been developed and clinically investigated at Osaka University Hospital. Their technique uses the cell sheet technology developed by Okano’s group of Tokyo Women’s Medical University to construct muscle cell sheets and attach them to the surfaces of the damaged hearts [15,16]. Shimizu et al. used temperature-sensitive culture dish surfaces and support materials to develop the two-dimensional manipulation of functional cardiac myocyte sheets, which demonstrated a heart tissue-like structure and indicated electrical pulsatile amplitude [17]. Sawa et al. produced such cell sheets from human tibialis anterior muscle and used them for the treatment of damaged hearts; however, the skeletal myoblasts could not beat synchronously with the host myocardium in vitro and could not functionally perform together [18]. Itabashi el al. also revealed that some of the skeletal myoblasts had automaticity but contracted independently and not synchronously as a single tissue, because the skeletal myoblast was electrically isolated from the surrounding myocardium and the electrical stimulation-induced excitation did not extend within skeletal myoblast sheets [19].
Takahashi and Yamanaka reported the latest development using induced pluripotent stem (iPS) cells, which can be differentiated into various types of
cells, such as cardiomyocytes, nerve cells, and cartilage [20]. Since then, a lot of research has been conducted to show that cardiomyocytes derived from iPS cells demonstrate functional, electrophysiological, and microstructural similarities to natural cardiomyocytes [21]. Sawa and Miyagawa developed cardiomyocyte sheets derived from human iPS (hiPS) cells and showed that they had the ability to contract synchronously in vitro and vivo [22]. It was also shown that a transplantation of hiPS cells was able to functionally recover the upregulated electrical potential of damaged heart tissue areas in large [23] and small [24] animal MI models. Kawamura et al. also reported that hiPS cell transplantation contributed significantly to an increase in cardiomyocyte function in damaged heart tissue [25]. Finally, just recently, hiPS cell derived cardiomyocyte (hiPS-CM) cell sheets were transplanted into the damaged heart of a MI patient. Although the clinical application of hiPS-CM cell sheets has successfully been conducted, the mechanical effects of such cell sheet transplantations have not yet been clearly understood.
On the other hand, dynamic finite element analyses of the heart have actively been conducted to understand the mechanical functions of the vital organ [26]. Finite element (FE) models have been used to investigate the effects of injecting a biocompatible material into the wall of the left ventricle (LV) to combat the progression of heart failure [27,28]. Wenk et al. developed an ellipsoidal LV FE model to study the optimal distribution of multiple spherical injectates [29]. Miller et al. [30] and Kortsmit et al. [31] also modelled the striated and bulk injectate distribution observed preclinically [32-34], as the discrete sheet-like structures embedded within the myocardium in a human LV model and a canine biventricular model, respectively. Sirry et al. presented a more realistic microstructurally detailed geometry of striated polyethylene glycol hydrogel injectate in an infarcted rat heart [35]. However, computational analyses of regenerative therapy of the heart using cell sheet technology have not yet been conducted.
The aim of this study, therefore, was to develop simple 3D models of a human LV to study the effects of MI on its beating behavior, and furthermore to model and analyze the mechanical effects of cell sheets attached to the damaged areas of the heart with MI.
2. Methods
2.1 Development of simple 3D models of normal and damaged human hearts
A 3D finite element (FE) model of a simplified left ventricle (LV) of human heart was constructed using 3D CAD software JVision 3.6 (Liverware Software, Livermore, CA) as shown in Figure 1. The dimensions of the LV model were determined from the references [36-39], and the length, diameter and thickness were set to 120.0, 40.0, and 6.0 mm, respectively. The FE heart model consisted of total 2703 nodes and 1800 hexahedral elements with 8 nodes. An anisotropic heart model was used to express the dynamic pulsation behavior of the elements of the LV model. The mathematical modeling of the heart model is described in the following section.
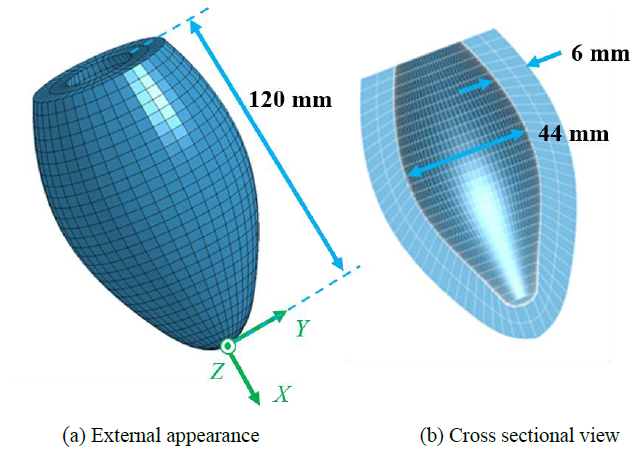
Figure 1: 3D model of simplified left ventricle
A simple MI model of square shape was then introduced into the LV model to imitate a damaged heart tissue as shown in Figure 2. The material model of MI was assumed to be the standard linear elastic solid with Young's modulus of 1 or 10 Pa to assess the effect of the modulus on the pulsation behavior, and Poisson’s ratio of 0.4. Three different sizes of the MI model were also considered by changing the number of elements, namely, Small with 2x2 elements, Medium with 4x4 elements, and Large with 8x8 elements as shown in Fig.2. Three different positions of Small MI (2x2) were also introduced into the LV model as shown in Figure 3. The MI model was located inside (Endocardial), outside (Epicardial) or through thickness (Transmural).
As a regenerative therapy model, a simple, square-shape cardiac tissue patch, imitating the iPS derived cardiac cell sheet, was introduced into the LV model with the transmural MI as shown in Figure 4. The FE model of the cardiac tissue patch was developed by creating new elements attached to the surface of the LV model and fully covering the MI model. The patch and the MI models consisted of 10x10 and 4x4 elements, respectively.
In the present dynamic FE analysis, the self-pulsation induced by the sarcomeres of cardiac cells was simulated using the anisotropic heart model, and no external force related to blood pressure was considered. Therefore, no mechanical boundary condition was given to the LV model. As the geometric boundary condition, all the nodes of the top surface of the LV model were fixed in the X-direction as shown in Figure 5. These FE models were then exported to the dynamic finite element code LS-DYNA (Liverware Software, Livermore, CA) to conduct the dynamic finite element analysis.
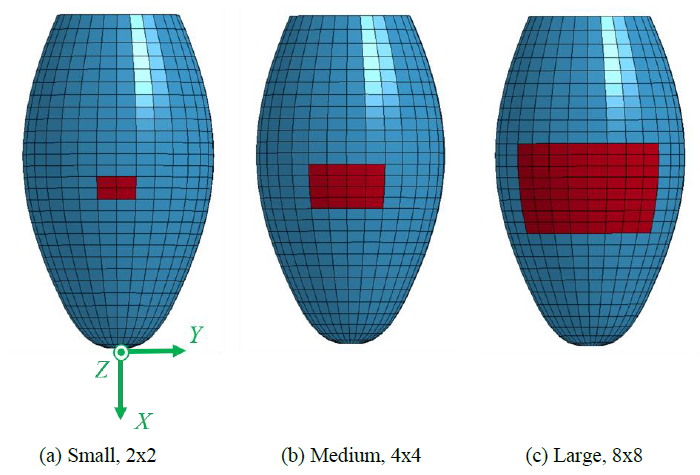
Figure 2: 3D LV model with three different MI models.
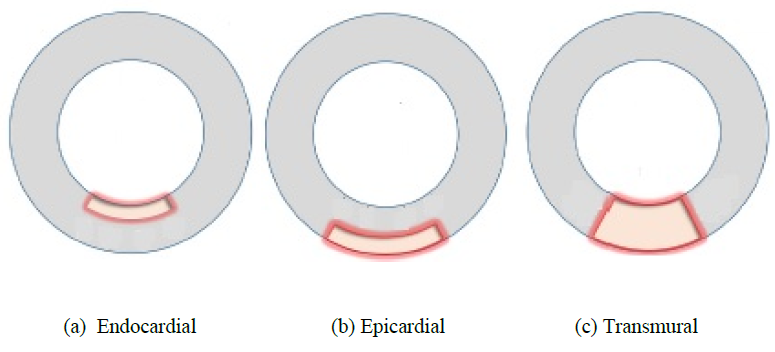
Figure 3: MI models with different positions (cross sectional view from top).
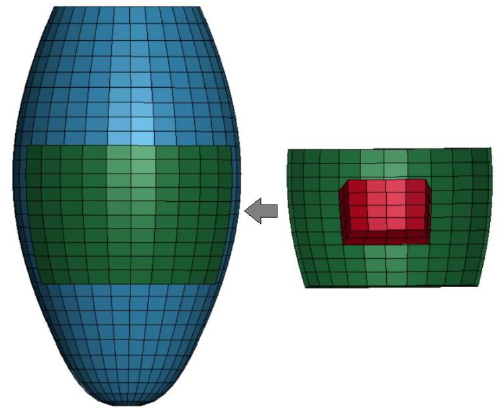
Figure 4: Regenerative therapy model with 4x4 MI and 10x10 cell sheet patch.
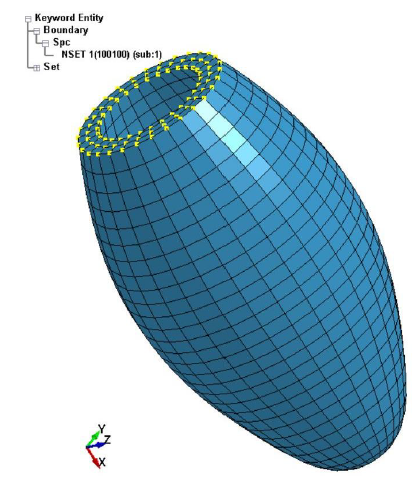
Figure 5: Geometric boundary condition of the LV model.
2.2 Modelling of active stress induced by sarcomeres
The normal heart tissue and the cardiac cell sheet patch were modeled using the anisotropic heart material model in order to simulate the pulsation behavior activated micromechanically by sarcomeres. This heart tissue model was developed by setting proper parameters for the Guccione’s model to regenerate the active beating behavior of the left ventricle without blood pressure [40-42]. The macroscopic mechanical behavior was assumed to be hyperelastic, and the active compressive stress component was added into the equation which correlates the stress components with the strain energy potential. The strain energy potential, W, that is anisotropic relative to the local fiber direction is defined by:

where C is a material constant, and Q is defined by:
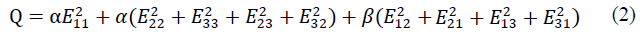
where α and β are the material constants, and Eij (i,j = 1,2,3) are the Green strain components. The active stress, T0, is then defined by:
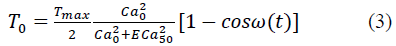
where
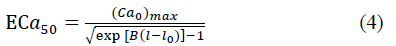
and
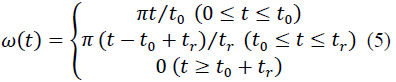
With
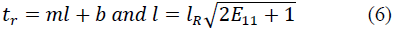
where T max is the isometric tension achieved at the longest sarcomere length, and Ca0 and (Ca0) max are the dynamic variation of calcium intracellular concentration and the maximum peak intracellular calcium concentration, respectively. B, m and b are constants, l is the sarcomere length and l0 and lR are the sarcomere length values at which no active tension develops and in the unloaded reference configuration, respectively. From Eqs. (1), (2) and (3), the second Piola-Kirchhoff stress tensor is defined as the sum of the passive stress derived from the strain energy function and the active stress component T0:
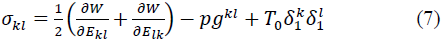
where p is the hydrostatic pressure to enforce the kinematic constraint, δ1k the Kronecker delta, and gkl the contravariant metric tensor referred to fiber coordinates and defined by:
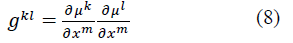
where μk is the fiber coordinates and xm are deformed rectangular Cartesian coordinates.
In the present FE modeling, the fiber direction was set to the circumferential direction, and therefore, the elements of the anisotropic heart model tended to shrink towards that direction. Hence, the entire LV model tended to elongate in the longer direction.
3. Results and discussion
Pulsation behavior of simple LV model:
The deformed images of the normal LV model are shown in Figure 6. It is seen that the pulsation behavior was clearly regenerated by introducing the time-dependent active stress component. The LV model elongated in the longer direction due to the shrinkage of all the elements in the circumferential direction. The X-displacements of the LV model is also shown in Figure 7. The time interval of the first pulsation is 1.6 s, and the maximum value of X-displacement is 13.8 mm which is much larger than that of Y and Z-displacement (the maximum value is 2.35 mm). Therefore, in the following sections, the X-displacement was chosen to be compared in order to examine the effects of the size, location and Young’s modulus of MI.
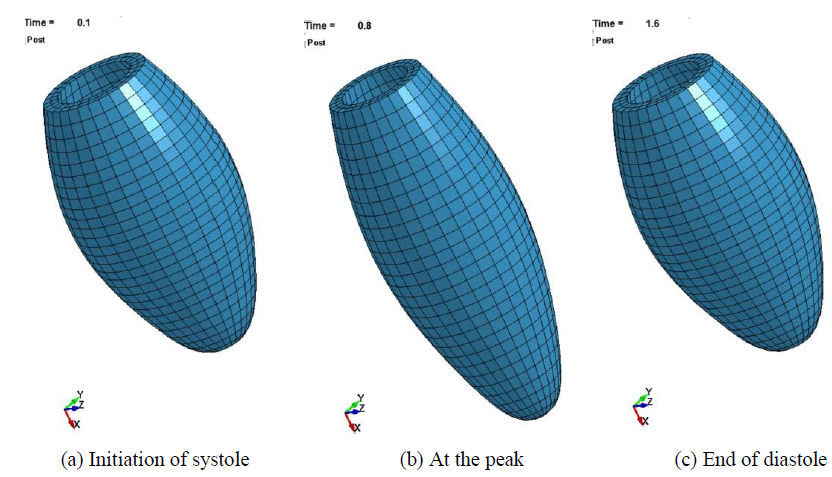
Figure 6: Beating behavior of the LV model.
3.1 Effects of MI on the pulsation behavior of LV model
Time-dependent behavior of X- displacement of the normal and the damaged LV models with three different MIs (Young’s modulus: 1Pa) are shown in Figure 8. It is clearly seen that the pulsation behavior tends to degrade with the existence of MI. Furthermore, the degree of degradation obviously increases as the size of MI increases. The effects of MI size and Young’s modulus of MI on the maximum X-displacements are shown in Figure 9. It is understood that the maximum displacement significantly decreases with increases of both MI size and Young’s modulus. The smallest decrease is about 8 % in the 2x2 MI with 1 Pa modulus model, while the largest decrease is about 77 % in the 8x8 MI with 10 Pa model.
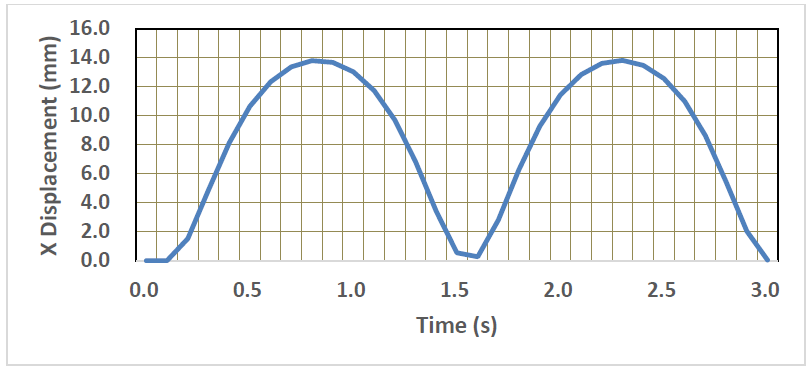
Figure 7: Time-variation of X-displacement of the LV model.
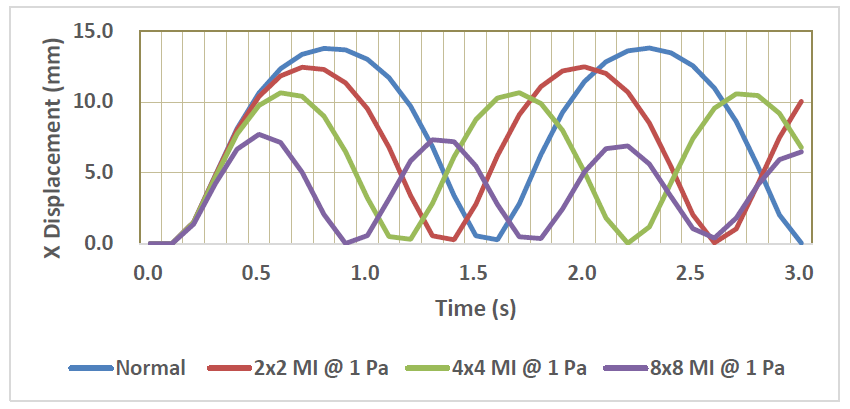
Figure 8: Time-variation of X-displacement of the normal and MI models.
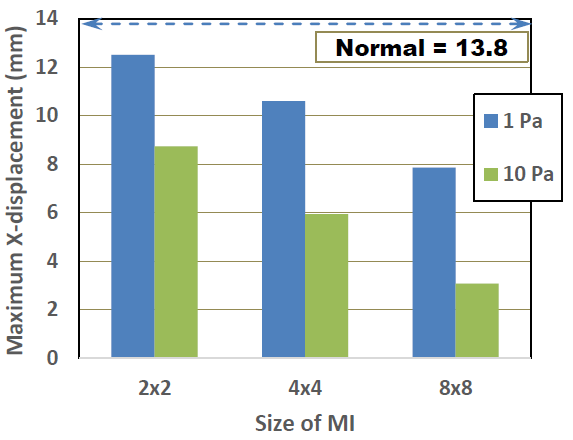
Figure 9: Effects of MI size and Young’s modulus on maximum X-displacement.
The effects of MI location and Young’s modulus on the maximum X-displacements are shown in Figure 10. Although the transmural MI exhibits the largest decrease, the differences between the three MI locations were not so significant. It is naturally understood that the transmural MI results in the worst case, as the damage is spread across the whole thickness. The damaged regions of both the endocardial and epicardial models cover only half the thickness, leaving normal healthy cardiac tissue in the other half thickness. The pulsation motion of the half normal region is restrained however, by the damaged tissue which is modelled as a linear elastic material and therefore, the degradation behaviors in the endocardial and epicardial are considered to be comparable to that of the transmural.
If sudden blockage occurs in the coronary artery, it can result in an inadequate supply of oxygenated blood to the myocardium, leading to myocardial necrosis [7]. This also affects the cardiac mechanics by causing regional myocardial dysfunction, increasing myocardial stiffness, and finally leading to heart failure [7, 43]. Mazumder R. et al. studied the stiffness of cardiac tissues using magnetic resonance elastography, which is a noninvasive imaging technique for measuring soft-tissue stiffness in vivo and concluded that the myocardial infarcts were much stiffer than the remote myocardium [7]. In a clinical study, Zhang H. et al. also found that the pulsation function is depressed when MI occurs, and that the condition becomes much worse when the MI size and stiffness also increase [44]. The results of the present simulation using the simple LV model with the simplified MI models are reasonably comparable with those experimental and clinical studies, suggesting that the simulation models can be used to predict such cardiac problems on the mechanical performance of the heart.
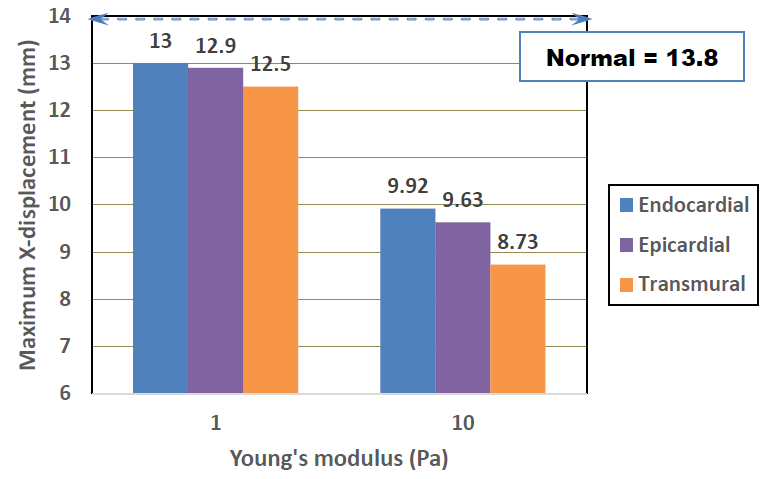
Figure 10: Effects of MI type and Young’s modulus on maximum X-displacement.
3.1 Effects of regenerative therapy with cardiac patch on pulsation behavior
The displacements of the six nodes shown in Figure 11 were used to assess the effects of the regenerative therapy on the dynamic pulsation motion. The displacement vectors at the point D, E and F are shown in Figure 12. The green, red and blue arrows indicate the normal, MI, and patch therapy models, respectively. It is clearly seen that the length and direction of the red arrow (MI model) are very different from those of the green arrow (normal model), indicating that the displacement of those surface nodes are disturbed by the existence of the MI model which cannot generate the autogenous pulsation movement. Although the length of the blue arrow (patch therapy model) is till shorter than that of the green arrow at all the three nodes, the direction of the blue arrow becomes close to that of the green arrow, suggesting that the existence of the cardiac cell sheet patch tends to recover the normal pulsation movement.
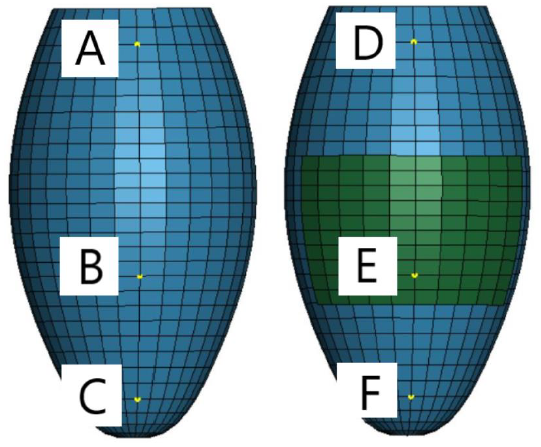
Figure 11: Six different points at which displacements were evaluated.
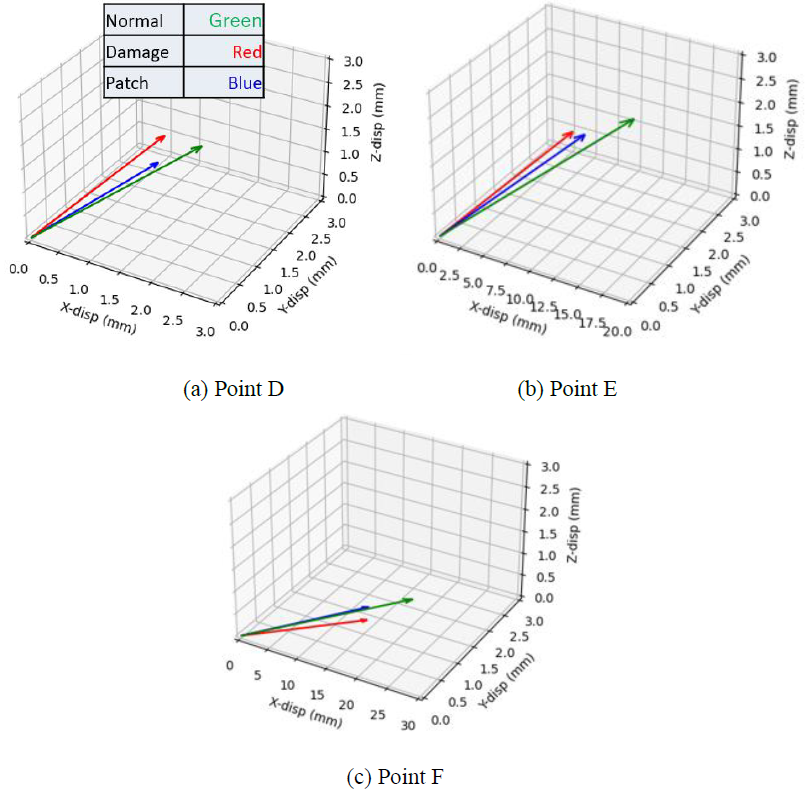
Figure 12: Displacement vectors at three different points. Green, Red, and Blue arrows indicate the normal, MI, and patch therapy models, respectively.
Differences of the displacement components between two nodes located at the opposite positions were also calculated in order to examine the symmetric deformation behavior of the LV model. Three sets of nodes, A-D, C-E and D-F (see Figure 11) were examined in this analysis. The results are summarized in Table 1. In the normal model, all the three sets exhibit no difference, indicating that the pulsation motion is purely symmetric. On the contrary, the MI model shows some differences in almost all the displacement components. Thus, the pulsation motion of the MI model can be understood as an asymmetric motion. Although the patch therapy model still exhibits slight asymmetry, the differences are much smaller than those of the MI model. Especially, the differences of X-displacement at all the three sets become zero, while the MI model has 1.7 mm at C-E and 0.9 mm at D-F.
|
Points |
Model |
X-displacement (mm) |
Y-displacement |
Z-displacement |
|
(mm) |
(mm) |
|||
|
A-D |
Normal |
0 |
0 |
0 |
|
MI |
0 |
-0.084 |
-0.8 |
|
|
Patch therapy |
0 |
0 |
0.01 |
|
|
Normal |
0 |
0 |
0 |
|
|
C-E |
MI |
1.7 |
0.015 |
0.14 |
|
Patch therapy |
0 |
-0.01 |
-0.08 |
|
|
Normal |
0 |
0 |
0 |
|
|
D-F |
MI |
0.9 |
0.087 |
0.83 |
|
Patch therapy |
0 |
0.012 |
0.12 |
Table 1: Difference of displacement components.
It is known that clinically, cell sheet patches have the ability to contract synchronously in hearts, and also repair heart disease such as myocardial infarction. According to Ishida et al. and Minami I. et al., regenerative patches using iPS-derived cardiac cells are able to repair MI without ethical concerns [45,46]. Our simulation results successfully showed slight recovery of dynamic pulsation motion by introducing the cardiac patch of square shape. In the actual clinical situations, such cardiac patches also have biological effects on the damaged heart tissue and will recover the pulsation motion more effectively. According to Guo R. et al, patch implementation is essential to improve cardiac function in terms of contraction [16]. Based on previous studies related to myocardial infarction of the animal model, the patch greatly improved systolic function, and to a certain degree also improved diastolic function [15,47].
5. Conclusion
In conclusion, a dynamic finite element model of the left ventricle was developed using Guccione’s active stress model. Pulsation behavior of the heart was successfully simulated using this heart model. Myocardial infarction model was introduced into the heart model as a damaged tissue. It was seen that larger damaged areas with greater Young's moduli resulted in decreasing the maximum displacement of pulsation. Different locations of damaged tissue were also introduced into the heart model. It was seen that the transmural type of MI results in a poorer outcome, when compared to the endocardial and epicardial type. Regenerative therapy was also modelled, by introducing a regenerated cardiac patch onto the damaged heart surface. This study found that such patch therapy is able to restore pulsation functions somewhat close to the normal condition.
Disclosure Statement
Dr. Mitsugu Todo has nothing to disclose.
References
- Chiong M, Wang ZV, Pedrozo Z, et al. Cardiomyocyte death: mechanisms and translational implications. Cell death & disease 2 (2011): 244.
- Cascio WE, Johnson TA, Gettes LS. Electrophysiologic changes in ischemic ventricular myocardium: I. Influence of ionic, metabolic, and energetic changes. Journal of cardiovascular electrophysiology 6 (1995): 1039-1062.
- Yusuf S, Reddy S, Ounpuu S, et al. Global burden of cardiovascular diseases. Part II. Variations in cardiovascular disease by specific ethnic groups and geographic regions and prevention strategies. Circulation 104 (2001): 2855–2864.
- Paiva L, Providência R, Barra S, et al. Universal definition of myocardial infarction: clinical insights. Cardiology 131 (2015): 13-21.
- Mozaffarian D, Benjamin EJ, Go AS, et al. Writing Group Members. Turner; American Heart Association Statistics Committee; Stroke Statistics Subcommittee. Heart disease and stroke statistics—2016 update: A report from the American Heart Association. Circulation 133 (2016): 38-60.
- Mangion K, Gao H, Husmeier D, et al. Advances in computational modelling for personalised medicine after myocardial infarction. Heart 104 (2018): 550-557.
- Mazumder R, Schroeder S, Mo X, et al. In Vivo Magnetic Resonance Elastography to Estimate Left Ventricular Stiffness in a Myocardial Infarction Induced Porcine Model. Journal Magnetic Resonance Imaging 45 (2017): 1024–1033.
- Chen J, Zhan Y, Wang Y, et al. Chitosan/silk fibroin modified nanofibrous patches with mesenchymal stem cells prevent heart remodeling post-myocardial infarction in rats. Acta biomaterialia 80 (2018): 154-68.
- Velagaleti RS, Pencina MJ, Murabito JM, et al. Long-term trends in the incidence of heart failure after myocardial infarction, Circulation 118 (2008): 2057-2062.
- Kikuchi K, Poss KD. Cardiac regenerative capacity and mechanisms. Annual review of cell and developmental biology 28 (2021): 719-741.
- Vunjak-Novakovic G, Lui KO, Tandon N, et al. Bioengineering heart muscle: a paradigm for regenerative medicine. Annual review of biomedical engineering 13 (2011): 245-267.
- Liszka J, Haberka M, Tabor Z, et al. Two-dimensional speckle-tracking echocardiography assessment of left ventricular remodeling in patients after myocardial infarction and primary reperfusion. Archives of medical science: AMS 10 (2014): 1091.
- Ashtari K, Nazari H, Ko H, et al. Electrically conductive nanomaterials for cardiac tissue engineering. Advanced Drug Delivery Reviews 144 (2019): 162-179.
- Ma L, Murry CE. Heart regeneration. Nature 473 (2011): 326-335.
- Sawa Y, Miyagawa S. Present and future perspectives on cell sheet-based myocardial regeneration therapy. Biomed Res Int (2013): 583912.
- Guo R, Morimatsu M, Feng T, et al. Stem cell-derived cell sheet transplantation for heart tissue repair in myocardial infarction. Stem Cell Research & Therapy 11 (2020): 191-193.
- Jackson KA, Majka SM, Wang H, et al. Regeneration of ischemic cardiac muscle and vascular endothelium by adult stem cells. The Journal of clinical investigation 107 (2001): 1395-1402.
- Toma C, Pittenger MF, Cahill KS, et al. Human mesenchymal stem cells differentiate to a cardiomyocyte phenotype in the adult murine heart. Circulation 105 (2002): 93-98.
- Kehat I, Kenyagin-Karsenti D, Snir M, et al. Human embryonic stem cells can differentiate into myocytes with structural and functional properties of cardiomyocytes. The Journal of clinical investigation108 (2001): 407-414.
- Mummery CL, Zhang J, Ng ES, et al. Differentiation of human embryonic stem cells and induced pluripotent stem cells to cardiomyocytes: a methods overview. Circulation research 111 (2012): 344-358.
- Dimmeler S, Burchfield J, Zeiher AM. Cell-based therapy of myocardial infarction. Arteriosclerosis, thrombosis, and vascular biology 28 (2008): 208-216.
- Zimmermann WH, Eschenhagen T. Cardiac tissue engineering for replacement therapy. Heart failure reviews. 8 (2003): 259-269.
- Chaudhuri R, Ramachandran M, Moharil P, et al. Biomaterials and cells for cardiac tissue engineering: current choices. Materials Science and Engineering: C 79 (2017): 950-957.
- Savoji H, Mohammadi MH, Rafatian N, et al. Cardiovascular disease models: a game changing paradigm in drug discovery and screening. Biomaterials 198 (2019): 3-26.
- Taylor DA, Sampaio LC, Gobin A. Building new hearts: a review of trends in cardiac tissue engineering. American Journal of Transplantation14 (2014) :2448-2459.
- Noble, D. Modeling the heart: from genes to cells to the whole organ. Science 295 (2002): 1678–1682.
- Wall ST, Walker JC, Healy KE, et al. Theoretical impact of the injection of material into the myocardium: a finite element model simulation. Circulation 114 (2006): 2627-2635.
- Wenk JF, Wall ST, Peterson RC, et al. A method for automatically optimizing medical devices for treating heart failure: designing polymeric injection patterns. Journal of biomechanical engineering 131 (2009).
- Wenk JF, Wall ST, Peterson RC, et al. A method for automatically optimizing medical devices for treating heart failure: designing polymeric injection patterns. Journal of biomechanical engineering 131 (2009).
- Miller R, Davies NH, Kortsmit J, et al. Outcomes of myocardial infarction hydrogel injection therapy in the human left ventricle dependent on injectate distribution. International journal for numerical methods in biomedical engineering 29 (2013): 870-874.
- Kortsmit J, Davies NH, Miller R, et al. Computational predictions of improved of wall mechanics and function of the infarcted left ventricle at early and late remodelling stages: comparison of layered and bulk hydrogel injectates. Advances in Biomechanics & Applications 1 (2014): 41.
- Kadner K, Dobner S, Franz T, et al. The beneficial effects of deferred delivery on the efficiency of hydrogel therapy post myocardial infarction. Biomaterials 33 (2012): 2060-2066.
- Dobner S, Bezuidenhout D, Govender P, et al. A synthetic non-degradable polyethylene glycol hydrogel retards adverse post-infarct left ventricular remodeling. Journal of cardiac failure 15 (2009): 629-636.
- Ifkovits JL, Tous E, Minakawa M, et al. Injectable hydrogel properties influence infarct expansion and extent of postinfarction left ventricular remodeling in an ovine model. Proceedings of the National Academy of Sciences 107 (2010): 11507-11512.
- Sirry MS, Davies NH, Kadner K, et al. Micro-structurally detailed model of a therapeutic hydrogel injectate in a rat biventricular cardiac geometry for computational simulations. Computer methods in biomechanics and biomedical engineering 18 (2015): 325-331.
- Kalsi KK, Smolenski RT, Pritchard RD, et al. Energetics and function of the failing human heart with dilated or hypertrophic cardiomyopathy. European journal of clinical investigation. 29 (1999): 469-477.
- Pascual M, Pascual DA, Soria F, et al. Effects of isolated obesity on systolic and diastolic left ventricular function. Heart 89 (2003): 1152-1156.
- Mohammadi S, Hedjazi A, Sajjadian M, et al. Study of the normal heart size in Northwest part of Iranian population: a cadaveric study. Journal of cardiovascular and thoracic research 8 (2016): 119.
- Narayanan K, Reinier K, Teodorescu C, et al. Left ventricular diameter and risk stratification for sudden cardiac death. Journal of the American Heart Association 3 (2014): e001193.
- Walker JC, Ratcliffe MB, Zhang P, et al. MRI-based finite-element analysis of left ventricular aneurysm. American Journal of Physiology-Heart and Circulatory Physiology 289 (2005): H692-700.
- Costa KD, Hunter PJ, Wayne JS, et al. A three-dimensional finite element method for large elastic deformations of ventricular myocardium. II. Prolate spheroidal coordinates. J Biomech Eng 118 (1996): 464–472.
- Guccione JM, Costa KD, McCulloch AD. Finite element stress analysis of left ventricular mechanics in the beating dog heart. Journal of biomechanics 28 (1995): 1167-1177.
- Angeli FS, Shapiro M, Amabile N, et al. Left ventricular remodeling after myocardial infarction: characterization of a swine model on beta blocker therapy. Comp Med 59 (2009): 272–279.
- Zhang H, Chen X, Gao E, et al. Increasing cardiac contractility after myocardial infarction exacerbates cardiac injury and pump dysfunction. Circulation research 107 (2010): 800-809.
- Ishida M, Miyagawa S, Saito A, et al. Transplantation of human-induced pluripotent stem cell-derived cardiomyocytes is superior to somatic stem cell therapy for restoring cardiac function and oxygen consumption in a porcine model of myocardial infarction. Transplantation 103 (2019): 291.
- Minami I, Yamada K, Otsuji TG, et al. A small molecule that promotes cardiac differentiation of human pluripotent stem cells under defined, cytokine and xeno-free conditions. Cell Rep 2 (2012): 1448–1460.
- Miki K, Uenaka H, Saito A, et al. Bioengineered myocardium derived from induced pluripotent stem cells improves cardiac function and attenuates cardiac remodeling following chronic myocardial infarction in rats. Stem Cells Transl Med 1 (2012): 430–437.


 Impact Factor: * 5.3
Impact Factor: * 5.3 CiteScore: 2.9
CiteScore: 2.9  Acceptance Rate: 11.01%
Acceptance Rate: 11.01%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 