Article Information

Godom Moise^1*, Tchouassi Gérard²

¹Doctor of Economics, University of Yaoundé II, XH7P+FMR, Soa, Cameroon

²Lecturer in Economics, University of Yaoundé II, XH7P+FMR, Soa, Cameroon

^*Corresponding Author: Godom Moise, University of Yaoundé II, XH7P+FMR, Soa, Cameroon.

Received: 14 May 2024; Accepted: 30 May 2024; Published: 10 June 2024

Citation: Godom Moise, Tchouassi Gérard. Modeling the Effects of Climate Change on Rice Yields in Cameroon: The Future?. International Journal of Plant, Animal and Environmental Sciences. 14 (2024): 31-41.

Abstract

Keywords

Climate change; ARDL model; Rice; Far North of Cameroon

Article Details

1. Introduction

Rice is currently one of the staple foods of Cameroon's rural and urban populations. According to Minader [2], demand was estimated at 576,949 tonnes, while local production stood at 140,710 tonnes (74% of which came from the far north). The remaining 436,239 tonnes are essentially imported to satisfy this excess demand. In 2022, local production will be 100,000 tonnes, down on 2020, when imports will be around 400,000 tonnes to meet national demand of almost 500,000 tonnes. According to this data, local rice production meets only 24% of national demand, which is partly justified by the precariousness of local production, as decried by Charbolin [3] since 1976, which can now be explained by several factors. Among rice production factors, the following remain paramount: the presence of flooded soil rich in organic matter [4], fertilizer inputs [5], regular rainfall requirements [6-8] and regulation of minimum and maximum temperatures [4]. In the literature, irregularities or uncontrolled variations in rainfall and temperature represent climate change, which refers to a global and continuous modification of the Earth's climatic and meteorological characteristics due to anthropogenic greenhouse gas emissions [9,10]..

Climate change is felt across the planet on physical, biological and human systems. Thus, it presents adverse consequences on several levels: negatively impacts social life by causing migration growth [11], exacerbates gender inequality [12], impacts human health and constitutes substantial loss of life [13], is among the causes of interpersonal conflict and socio-political unrest [14,15] and stimulates reduced agricultural productivity and economic growth [16]. It should be noted that African farming systems, mainly rain-fed, are still highly dependent on unpredictable climate change [17,18]. The accelerating pace of climate change, combined with global population growth, income contractions and agricultural vulnerabilities, threatens food security everywhere [19,20].

Beyond the work on climate change and socio-economic aspects, it should be noted that agriculture's particular vulnerability to climate change is reflected in higher temperatures, which are likely to reduce the yields of certain crops via the proliferation of weeds, flies, locusts, crop-damaging rats [19]. It has also been observed that yields of crops such as wheat and maize have decreased as a result of rising temperatures. With this in mind, a study covering the period from 1980 to 2008 showed that yield reductions for certain cereals such as wheat and maize due to global warming are of the order of 6% and 4% respectively, but global soybean and rice yields were found to be relatively unaffected [21]. However, as the damage to climate change evolves, a study over the period from 2005 to 2012 showed that extreme temperature anomalies and reduced rainfall intensity during the rainy season affect flooded rice production in the Ndop tidewater in northwest Cameroon [8]. Thus, the effects of climate change on agriculture vary over time depending on crops, adaptation measures implemented and study regions [22].

The aim of this study is to highlight the dynamic effects of variations in temperature and rainfall on rice yields in the Far North of Cameroon. This concern reinforces the interest of this study, which focuses on the place of this zone (north and extreme north) in national production, and the verification of the temporal effects of temperature and rainfall variations using the ARDL estimation method. This study continues with the presentation of the literature review in section 2, the presentation of the methodology in section 3, the summary and discussion of the main results in section 4 and concludes with some economic policy recommendations.

2. Literature Review

The link between climate change and agricultural yields in general is not new. Theoretically, there are 3 approaches to estimating the relative effects of climate on agriculture : 1) An approach based on agroclimatic indices, e.g. rainfall indices known as the lamb index [23], which distinguish wetter years from less wet years, also enable us to study the influence of rainfall on agricultural crops : 2) crop simulation models based on climate models and crop models, which enable predictive estimates of the effects of climate variations on agriculture over time, and comparisons of their impacts between localities or periods [24] and 3) Statistical or econometric models that simultaneously take into account all factors likely to influence agricultural production or yields and are useful for assessing the impact of climate change in the real conditions of farmers who are characterized by suboptimal management of their agricultural activities [25]. Econometric and statistical models used in the field of climate change include multiple linear regression models to study the impact of climate change on farm incomes in Burkina Faso [26], the VAR model to study interactions between climate change, cotton prices and production in Cameroon [22], the ARDL panel model to study climate shocks on monetary policy in developing countries [27] and the ARDL model to study the effects of climate change on rice production in the Zou et al. collines [28] department in central Benin [28].

Using the agro-climatic model, Lobell and Gourdji [21] have shown that Climate variability exposes plant cells of different crops to insect pests and diseases that affect agricultural yields. The two authors point out that the climate variability described can be explained by the following factors: rising temperature, intensification of the Hydrological Cycle and increasing carbon dioxide (CO₂) concentration. The effect of rising temperatures on agricultural crops has been decried in the past by Mendelsohn and Schlesinger, who demonstrated that at certain temperature thresholds, crop yields tend to fall, and that the delay in the growth process leads to a deterioration in cereal yields. Later, studies of the interaction between climate and agriculture in the USA, using modifications of the standard Ricardian model [29] found that the value of irrigated cropland is not sensitive to rainfall, but increases in value with temperature [30]. They went on to note that climate also affects soil fertility and quality, the rate of plant respiration and the grain filling process, and by transitivity impacts yield. Analysis of the impact of climate change on wheat productivity in Pakistan, using the production function approach applied to data for the period 1981-2010 led to the conclusion that a 1°C increase in mean temperature during the sowing period would reduce crop yield by 7.4% [31]. A decade earlier, a study revealed that when farmers did not use climate change adaptation techniques, a 2°C increase in normal temperatures would lead to an 11% decrease in crop yields, and a 5% decrease in rainfall would cause a 4% increase in crop yields [32]. In most studies carried out in West Africa, the effect of climate change on crop yields is rather negative [33]. Thus, it is commonly accepted that climate change remains a factor affecting agricultural crops and livestock in Africa [34]. In the Zou et collines department in central Benin, the study by Ajavon Ayi et al. [28] showed that changes in rainfall and humidity affect rice production in the short and long term, using the ARDL model.

In summary, most of the studies presented above use projected data on climate change variables to stimulate its effects on crop and livestock yields via climate models. The drawback of these models is that they do not consider that atmospheric circulation is not deterministically predictable beyond a few days, since small-scale growth can contaminate the whole circulation [24] and the effects of change could vary over time. What's more, none of these studies examined the impact of climate change on rice yields in the far north of Cameroon. Given that in northern Cameroon, climate change is a real fact [35,36], the present study attempts to add value to the literature by using the econometric technique (specifically ARDL modelling) to see the effects over time of climate change on rice yield in the far north of Cameroon.

3. Study Methodology

This section presents data sources and empirical estimation strategies.

3.1. Presentation of variables and data sources

This study used variables such as rice yield (Rriz) as the explained variable, and temperature variation (TV) and rainfall variation (RfV) measured by their standard deviations to represent the phenomenon of climate change as the explanatory variables of interest, which are also used by Mpabé [22] to measure the impact of climate change on agricultural production. The other explanatory variables are : the annual growth rate of the rural population (AGRRP), which is regularly used in the literature to assess the role of labor in agricultural crops such as rice [3,16] domestic credit granted to the private sector (DCGPS) to finance inputs and phosphate fertilizer (PF) used for agricultural purposes, which represents an important element in improving soil fertility impacting rice yield [4,5].

Data on temperatures (in degrees Celsius) and monthly rainfall in the North and Far North regions of Cameroon are taken from the Work Bank Group Climate Change knowledge Portal database, and the standard deviations of each variable are calculated. Data on rice yields (RY) in Hg/ha converted to tonnes per hectare with reference to SEMRY data, and phosphate fertilizer inputs (in tonnes) are taken from the statistical database of the United Nations Food and Agriculture Organization (FAOSTAT). Data on the annual growth rate of the rural population (AGRP) and domestic credit granted to the private sector (DCGPS) are taken from the World Bank database (World Development Indicator). The study period extends from 1975 to 2021, which is long enough to perform a long-term analysis. In order to make the right choice of model, it is important to review the stationary test for the series of variables presented.

3.2. Stationarity testing of variable series

To study the stationary of variables used in econometric work, two categories of tests are used, namely the Augmented Dickey-Fuller (ADF) and Phillips Perron (PP) tests, the null hypothesis of which is non-stationary, and the Kwiatkowski-Phillips-Schmidt Shin (KPSS) test, the null hypothesis of which is stationarity [37]. The Dickey-Fuller test (1981) highlights the stationary or non-stationary nature of a series by determining a deterministic or stochastic trend through its sequential strategies (see Régie Bourbonais 7^th edition, page 174). The choice of this test is justified by the fact that not all variable series contain trend breaks [38] and that they are not decomposed into a deterministic trend and a random walk (KPSS test (1992)). Graphs 1 and 2 in the appendix show unbroken time series for all variables.

Table 1 shows that the variables rice yield (RY), phosphate fertilizer input and credit granted to the private sector are not stationary in level, but are integrated of order 1. On the other hand, the variables' rainfall variations (RfV), temperature variations (TV) and the annual growth rate of the rural population are stationary in level and are therefore integrated of order 0. In fact, not all the variables are integrated of the same order, so a model is needed that can take account of the realities obtained from the characteristics of these variables.

Source: Authors, based on estimates by Eviews 10

Table 1: Augmented Dickey-Fuller stationarity test for variables.

3.3 Choice of study model

For this study, given the properties of the variables that are integrated of different orders (RY(I1), VRf (I0), TV(I0) ect.), it could be that these variables will have influencing relationships over time. ARDL modeling therefore remains valid in this case. This modeling has been used in the near past by several authors to econometrically verify: i) the sustainability of public debt in Morocco during 1970-2018 [39]; ii) the effects of climate change on rice production in Benin [28]; iii) climate change shocks on monetary policy in developing countries [27]. These authors note that ARDL modeling can be used to test co-integration and estimate short- and long-term relationships when the series are not integrated to the same order. However, the choice of this model can be explained on two levels : (1) at the level of variable stationary, it was found that all six study variables are integrated in different orders, making it ineffective to use Engle and Granger's co-integration test and Johansen's test (which require the same order of variable integration) ; (2) the application of Pesaran et al. [1] bounds co-integration test, which remains the basis of the ARDL model [40] would provide long-term relationships between rice yield and variations in rainfall, temperature and other variables.

In general form, this ARDL model (p p' q r s u) in this study is therefore as follows:

Rrizt=φ+ + + + +εt; With t= (1975, 1976, 1977,......,2021) represents the sample, εt= measurement error at period t, φ= model constant, αi= coefficients of lagged rice yield values, β1j, β2l, β3m, β4n, β5z are respectively the coefficients of the variables rainfall variations, temperature variations, phosphate fertilizer supply, the annual growth rate of the rural population and domestic credit granted to the private sectors as well as their lagged values.

4. Presentation and Discussion of Results

4.1. Presentation of results

The presentation of the ARDL model estimation results includes the determination of the co-integration test steps of Pesaran et al. [1] on the one hand, and the short- and long-term dynamics enabling the study of the dynamic influence of variations in climate elements and other variables on rice yield in the northern zone of Cameroon on the other.

4.1.1 Co-integration test by pesaran et al. [1]

*Optimal offset and ARDL model estimation (p p' q r s u)

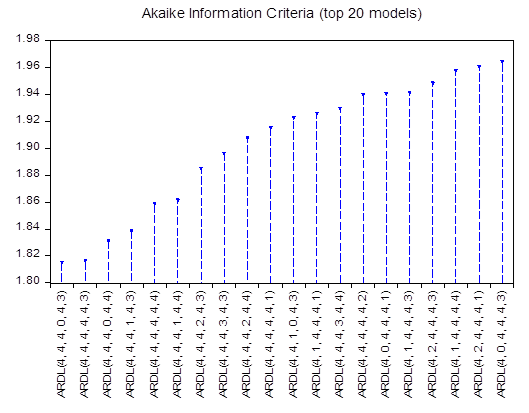
Akeike's information criterion was used to select the optimal ARDL model, the one offering statistically significant results with the least parameters. The graph used to select this optimal model is shown below.

Source: Authors, estimation by Eviews 10

Figure 1: Selection of the top 20 models according to Akaike.

As can be seen, the ARDL model (4,4,4,0, 4,3) is the most optimal of the 19 presented, offering the lowest Akeike value (1.82) and statistically significant results. The estimation results for the selected optimal ARDL model are therefore shown in Appendix Table 2.

Before commenting on the estimation results for the coefficients in Table 3, it is important to carry out the robustness tests first, namely the white noise test (Ljung_Box Q-statistic), the error autocorrelation test (Breush-Godfrey), the heteroscedasticity test (Breush-Pagan-Godfrey), the error normality test (Jarque-Bera) and the specification test (Ramsey RESET Test and CUSUM of square). The purpose of the white noise test is to check whether the residuals between the observed values and the values estimated by the model behave like white noise. At the end of this test, graph 3 in the appendix shows that, whatever the lag k among the 20 lags, the probability of the test is always greater than 0.05 and that the terms of the correlograms are contained in the two corridors (the first corridor is associated with autocorrelation and the other with partial autocorrelation). We can conclude that the estimation errors are white noise. The results of the diagnostic tests are summarized in Table 2 below.

Source: Authors, based on our calculations

Table 2: Model robustness test results.

Looking at all these tests, we note that the null hypotheses of error autocorrelation (Breush-Godfrey: serial correlation LM test) and heteroscedasticity (Breush-Pagan-Godfrey) are rejected. This means that in the estimated model, the errors are neither autocorrelated nor heteroscedastic (they are homoscedastic). The Jarque-Bera hypothesis of error normality is accepted, as its probability is greater than 5%. The model is well specified (by the Ramsey test, the probability of the Fisher statistic is greater than 5%). In short, the results of the various diagnostic tests lead to the validation of the ARDL model (4,4,4,0,4,3,). Although the estimated ARDL model is robust, it does not directly allow for immediate effects (short-term dynamics) or long-term effects. For this reason, it is recommended to perform the Co-integration test to see if rice yield is influenced by variations in rainfall and temperature, as well as by other variables.

** Co-integration test at bounds (Pesaran et al. [1]) and short- and long-term relationships (coefficients)

Source: Authors, based on our calculations

Table 3: Co-integration test at buns (Fisher)

The results of the Co-integration test at the bounds confirm the existence of a Co-integration relationship between the variables (as the value of F-stat is greater than that of the upper bound even at 1% : 4.47>4.15). The existence of a Co-integration relationship makes it possible to estimate the short- and long-term effects between variations in annual rainfall, variations in annual temperature, phosphate fertilizer input and population growth rate and rice yield.

4.1.2. Short-term dynamics, the adjustment coefficient and long-term coefficients

* Short-term coefficients and adjustment coefficient

Source: Auteurs, estimation by Eviews 10

Note: ***, ** and * represent significance at 1%, 5% and 10% respectively.

Table 4: Short-run coefficients and recall force.

In absolute terms, the adjustment coefficient is 0.730888, which means that we manage to adjust 73% of the imbalance between the desired level and the actual level of rice yield in the face of climatic hazards (specifically rainfall variations) and the annual growth rate of the rural population. The speed of adjustment would therefore be good in the relationship process following a shock from the previous year. In the short term (during the current year), for example, a 10% increase in rainfall variation causes a 3.6% drop in rice yield in northern Cameroon.

** Long-term coefficients

Source: Auteurs, estimation by Eviews 10

Note: ***, ** and * represent significance at 1%, 5% and 10% respectively

Table 5: Long-term estimation results.

As in the short term, the long-term coefficient of the variable variation in rainfall retains the same sign while remaining statistically significant even at 1%, and that of the growth rate of the rural population remains significant at 5%, but with the opposite sign to the short-term coefficient. On the other hand, the coefficients of the variables temperature variation, phosphate fertilizer input and credit granted to the private sector are insignificant even at 10% in the long term. The results obtained in the short and long term should therefore be discussed before concluding the study.

5. Discussion

Considering the results observed above in the short and long term, it must first be said that rainfall variations in the far north of Cameroon have negative short- and long-term effects on rice yields. This is shown by the fact that a variation of around 10% in rainfall results in rice yield decreases of around 3.6% and 1.14% respectively in the short and long term. Ajavon et al. [28] found similar results when studying the effects of climate change on rice production in Benin, and showed that changes in rainfall and humidity negatively affect rice production in the short and long term, using the ARDL model. These results confirm the theory that "rice cultivation requires a certain amount of rainfall, i.e. large quantities of water are needed to satisfy rice vegetative growth" mentioned in Brigitte Courtois' [6] studies, but without strong variations, as Antu et al. [13] showed from an analysis of coefficients of variation that variations in temperature and rainfall negatively affect rice production in the Ndop marsh in north-western Cameroon. In a similar vein, Godom and Numba [41] used a VAR model to show that violent increases in rainfall have a negative impact on rice yields in Cameroon. However, these studies have difficulty in measuring both short- and long-term effects at the same time. This study addresses the limitations of the studies by Antu et al. [13] and Godom and Numba [41] by identifying the short- and long-term effects on rice yields in the north and far north of Cameroon.

Temperature variations during the rainy season had no impact on rice yields in the northern zone of Cameroon, either in the short or long term. These results may indicate that, in this study area, variations around mean temperatures during the rainy seasons are negligible, and are justified by : (1) contractions in wet-season temperature variations of around 0.18 (see TV standard deviation in Appendix Table 1) are extremely low; (2) rice can manage the average of these variations, which is 1.75 (see TV average in Appendix Table 1), since beyond certain thresholds, temperature remains indispensable in improving rice yield [42]. With regard to the other variables taken into account in our study, only the variable annual growth rate of the rural population (AGRRP) shows significant impacts in the short and long term. However, it should be pointed out that these impacts are respectively negative and positive in the short and long term. The negative short-term impact means that the increase in rural population is not immediately beneficial for rice growing, but it will be in the future [43-61]. This is due to the contraction of the rice-growing workforce as a result of the increasing rural exodus: an increase in population is therefore needed to reinforce this workforce.

6. Conclusion and Recommendations

The aim of this study was to determine the effects of climate change on rice yields in the far north of Cameroon. In the literature, three approaches are generally used to study the effects of climate change on agricultural crops: the approach based on agro-climatic indices, crop simulation models based on climate models or crop models and statistical or econometric models. Statistical or econometric models are used to assess the impact of climate change under farmers' actual conditions, taking into account simultaneously all factors likely to influence agricultural production or yields [25]. Thus, given the statistical and econometric characteristics of the variables (RY, RfV, TV, PF, AGRRP and DCGPS), revealing that they are not integrated of the same order, we opted to use the cointegration test of Pesaran et al. [1], using ARDL modelling to estimate the short- and long-term effects of climate change on rice yield over the period 1975-2021.

The results of this study showed that : (1) variations in rainfall have negative short- and long-term impacts on rice yield ; (2) temperature variation in the far north of Cameroon during the rainy season has a low amplitude (0.18) and shows no impact in the short or long term, although it does have positive and negative coefficients in the short and long term ; (3) the rate of rural population growth has a negative impact on rice yield in the short term and a positive impact in the long term. In view of these results, it is important that farmers become aware of the negative dynamic effects of climate change on rice cultivation and apply more advanced rice-growing methods to resilience.

References

1. Pesaran MH, Shin Y, Smith RJ. Bounds Testing Approaches to the Analysis of Level Relationships, in Journal of Applied Econometrics 16 (2001): 289326.
2. Stratégie nationale de développement de la riziculture au Cameroun, Mouture II(2020).
3. Charbolin R. Le secteur expérimental de modernisation de la riziculture de Yagoua - SEMRY (2e partie). Horizon pleins textes. Publications des scientifiques de l'IRAD (1976).
4. Zingore S, Wairegi L, Kabirou MN. Guide pour la gestion des systèmes de culture de riz. Consortium Africain pour la Santé des Sols, Nairobi(2014).
5. Kone B. Effets des différentes sources de phosphate sur les rendements du riz sur sols acides (2010).
6. Courtois B. Une brève histoire du riz et de son amélioration génétique. Cirad, UMR1096, TA40/03 34398, Montpellier Cedex 5, France (2007).
7. Tabi FO, Adiku SGK, Ofori K, et al. Perceptions of rain fed lowland rice farmers on climate change, their vulnerability and adaptation strategies in the Volta Region of Ghana. SAT Journal 4 (2010): 2-4.
8. Antu VN, Nkwemoh CA, Tchawa P. The vulnerability of swamp rice production to the observed effects of rainfall and temperature variability in Ndop sub-division, Cameroon. Canadian Journal of Tropical Geography 3 (2013): 1-14.
9. Climate change: status of the 5^th IPCC report; Laboratoire des Sciences du Climat et de l'Environnement (LSCE), France (2015).
10. Climate Change 2022, Mitigation of Climate Change; Sixth Assessment Report (2022).
11. Berlemann M, Steinhardt MF. Climate Change, Natural Disasters, and Migration a Survey of the Empirical Evidence. CESifo Economic Studies 63 (2017): 353-385.
12. Eastin J. Climate Change and Gender Equality in Developing States. World Development 107 (2018): 289-305.
13. Meierrieks D. Weather Shocks, Climate Change and Human Health. World Development 138 (2021): 105228.
14. Carleton TA, Hsiang SM. Social and Economic Impacts of Climate. Science 353 (2016).
15. Harari M, Ferrara E. L. Conflict, Climate, and Cells: A Disaggregated Analysis. Review of Economics and Statistics (2018): 594-608.
16. Dell M, Jones BF, Olken BA. What Do We Learn from the Weather? The New Climate–Economy Literature; Journal of Economic Literature 52 (2014): 740-798.
17. Dinar A, Hassan R, Mendelsohn R, eta l. Climate Change and Agriculture in Africa: Impact Assessment and Adaptation Strategies. London: Earth scan Publishing (2008).
18. Seo SN, Mendelsohn R, Dinar A, et al. A Ricardian analysis of the distribution of climate change impacts on agriculture across agro-ecological zones in Africa. Environmental and Resource Economics 43 (2009): 313-332.
19. Nelson GC, Rosegrant MW, Koo J, et al. Climate change impact of agriculture and costs of adaptation. Food Policy Report, International Food Policy Research Institute (2012): 1-57.
20. Fomekong F. et Ngono G. Changements climatiques, production agricole et effets sur la population au Cameroun. Institut National de la Statistique, Cameroun (2011).
21. Lobell DB, Gourdji SM. The Influence of Climate Change on Global Crop Productivity. Plant Physiology 160 (2012): 271-280.
22. Mpabe MJB. Climate Change, Cotton Prices andProduction inCameroon; Association of Development Research and Training Institutes (EADI) (2021).
23. Lamb PJ. Persistence of Subsaharan drought. Nature London 299 (1982): 46-47.
24. Le Treut H. Comment je vois le monde, Evolution climatique: les modeles et leurs limites, edité par Le Treut, H., Jancovici, J., M., Effet de serre: allons-nous changer le climat? Editions Champs, Flammarion, (2004).
25. Rötter R, Höhn J. An overview of climate change impact on crop production and its variability in Europe, related uncertainties and research challenge. Edited by FAO (2015), Climate Change and Food Systems: Global Assessments and Implications For Food Security and Trade (2015): 107-145.
26. Ouedraogo M. Impact des changements climatiques sur les revenus agricoles au Burkina Faso, Journal of Agriculture and Environment for International Development 106 (2012): 3-21.
27. Eric TTJ, Joseph KM, Landry BJ. Changement climatique et politique monétaire dans les pays en développement; BEAC, direction des études, de la recherche et des statistiques (2022).
28. Ajavon Ayi YC, Kpatinnon N. R et TENTE AHB. Effets des changements climatiques sur la production du riz dans les départements du zou et des collines au centre du bénin, afrique de l’ouest. International Journal of Recent Advances in Multidisciplinary 07 (2020): 6024-6033.
29. Mendelsohn R, Nordhaus WD. The Impact of Global Warming on Agriculture: A Ricardian Analysis. American Economic Review 84 (1994): 753-71.
30. Mendelsohn R, And Dinar A. Climate, Water and Agriculture. Land Economics 79 (2003): 328-341.
31. Ahmad M, Siftain H, Iqbal M. Impact of Climate Change on Wheat Productivity in Pakistan: A District Level Analysis. IDRC Climate Change Working Paper Series No. 1 (2014).
32. Gbetibouo GA, HASSAN RM. Measuring the economic impact of climate change on major South African field crops: Ricardian approach”. Global and Planetary Change 47 (2005): 143-152.
33. Roudier P, Sultan B, Quirion P, et al. The impact of future climate change on West African crop yields: What does the recent literature say? Global Environmental Change 21 (2011): 1073-1083.
34. Molua EL. Climate change and African agriculture: Review of impact and adaptation choices. In: Kondlo and Ejiogu (Eds.), Governance in the 21^st Century, HRSC Press (2011).
35. Gerardeaux E Sultan B, Guiziou C, et al. Positive effect of climate change on cotton in 2050 by CO₂ enrichment and conservation agriculture in Cameroon, Agronomy for sustainable development 33 (2013): 485-495.
36. Loison R, Audebert A, Debaeke P, et al. Designing cotton ideotypes for the future: Reducing risk of crop failure for low input rainfed conditions in Northen Cameroon. European Journal of Agronomy 9 (2017): 162-173.
37. Ait Oudra, M. La modélisation des séries non stationnaires, la théorie de la cointégration: application à la demande de monnaie au Maroc.Thèse de Doctorat en Sciences Économiques FSJES – Fès(2006).
38. Benyacoub B, Es-Salmani M. Modélisation ARDL, test de cointégration aux bornes pour la vérification de la soutenabilité de la dette publique au Maroc. Revue Internationale du Chercheur 2 (2021): 1-24.
39. Phillips PCB, Perron P. Testing for a Unit Root in Time Series Regression. Biometrica 75 (1988): 335-46.
40. Kibala Kuma J. Modélisation ARDL, Test de cointégration aux bornes et Approche de TodaYamamoto: éléments de théorie et pratiques sur logiciels. Licence. Congo-Kinshasa.cel-01766214 (2018): 1-55.
41. Goodm M, Numba Changement climatique et rendement du riz au Cameroun, Recherches et Applications en Sciences Economiques et de Gestion 2 (2023): 12-30.
42. Gerardeaux E, Giner M. L’effet positif du changement climatique sur le riz à Madagascar (2012).
43. Arditi C. Quelques réflexions socio-économiques sur la riziculture irriguée dans le Nord Cameroun (SEMRY I et SEMRY II). In: Bulletin de l'Association française des anthropologues, N°. 20. Recherche et/ou développement (1985).
44. Auffhammer M, Ramanathan V, Vincent JR. Climate change, the monsoon, and rice yield in India. Climatic Change (2011).
45. Dobor L, Barcza Z, Hlásny T, et al. Crop planting date matters: Estimation methods and effect on future yields. Agricultural and Forest Meteorology 223 (2016): 103-115.
46. Frederic B. Contribution de l’agriculture africaine au changement climatique et potentiel d’atténuation. Grain de sel, N°. 49, janvier – mars (2010).
47. Gildas LD, EDJA AH, NOUATIN GS. Variation climatique et production vivrière : la culture du maïs dans le système agricole périurbain de la commune de Parakou au Nord-Benin ». Afrique Science 11 (2015): 183-194.
48. Granger CWJ, NEWBOLD P. Spurious regression in econometrics, Journal of Econometrics 2 (1974): 111-120.
49. HORIE T. Global warming and rice production in Asia: Modeling, impact prediction and adaptation. Proc Jpn Acad Ser B Phys Biol Sci 95 (2019): 211244.
50. Jeder H, Khalifa AB, Sghaier M. Impact des changements climatiques sur l’agriculture dans la plaine de Jeffara au sud-est tunisien; Journal of Agriculture and Environment for International Development - JAEID 2013 107 (2013): 229-242.
51. Climate change assessment. Contribution of Working Groups I, II and III to the IPCC Fourth Assessment Report, UNEP, Geneva (2007).
52. Jagoret P, Todem H, Ngogue E, et al. Diversification des exploitations agricoles à base de cacaoyer au Centre Cameroun : mythe ou réalité? Biotechnol Agron Soc Environ 13 (2009): 271-280.
53. Johansen S. Statistical Analysis of Cointegrating Vectors, in Journal of Economic Dynamic and Control 12 (1988): 231-254.
54. Kanohin FO, Saley MB, Ake GE, et al. Variabilité climatique et productions de café et cacao en zone tropicale humide : cas de la région de Daoukro (Centre-est de la Côte d’ivoire); International Journal of Innovation and Applied Studies 1 (2012): 194-215.
55. Kwiatkowski D, Phillips PCB, Schmidtet P, et al. Testing the Null Hypothesis of Stationarity against an Alternative of a Unit Root: How Sure Are We that Economic Time Series Have a Unit Root?. Journal of Econometrics 54 (1992): 159-78.
56. Maddison D, Manley M, Kurukula SP. The Impact of Climate Change on African Agriculture: A Ricardian approach. World Bank, Policy Research Working Paper, N° 4306 (2007).
57. Rhys HJ, Westra SP, Sharma A. Observed relation between extreme sub-daily precipitation, surface temperature, and relative humidity. Geophysical Research Letters 37 (2010): L22805.
58. Sie M. Analyse des contraintes photo-thermiques en vue de l'adaptation des variétés de riz irrigué au Sahel. Thèse de doctorat, Montpellier, France, Ecole Nationale Supérieure d'Agronomie (1997).
59. Sultant B. L'agriculture face au défi du changement climatique: l'exemple du Sahel. Metis UMB/7619 (2016).
60. Tingem M, Rivington M, Bellocchi G, et al. Effects of climate change on crop production in Cameroon. Inter-Research Science Publisher 36 (2003): 65-77.
61. Trnka M, Olesen JE, Kersebaum KC, et al. Agroclimatic conditions in Europe under climate change. Global Change Biology 17 (2011): 2298-2318.

Appendices

Source: Authors, based on our estimates by Eviews 10

Table 1: Descriptive statistics for variables.

Source: Authors, based on our estimates by Eviews 10

Note: ***, ** and * represent significance at 1%, 5% and 10% respectively).

Table 2: Estimation of ARDL model coefficients (4,4,4,0,4,3).

Source: Authors, based on our estimates by Eviews 10

Graph 1: Trends in rice yields, temperature variations and annual rural population growth.

Graph 2: Trends in domestic credit granted to the private sector and variations in rainfall.

Source: Authors, based on our estimates by Eviews 10