The Fastest Simulation of Protein Folding Based on Torsion Angles
Article Information
Sunghoon Jung*
Seoul National University, Seoul, Republic of Korea
*Corresponding Authors: Sunghoon Jung, Inhun Officetel, 3Gil 8, Nakseongdae-ro, Guanak-gu, Seoul, Republic of Korea
Received: 12 January 20201; Accepted: 17 February 20201; Published: 22 February 20201
Citation: Sunghoon Jung. The Fastest Simulation of Protein Folding Based on Torsion Angles. Journal of Bioinformatics and Systems Biology 4 (2021): 1-12.
View / Download Pdf Share at FacebookAbstract
Backgrounds: Enormous number of possible conformations in the protein structure simulation have led molecular dynamics researchers to be frustrated until now. Some methods with defects ended their experiments into failure. This made them fail to determine the structure and function of folded protein in stable state with the lowest potential energy. This apparently exist in nature. The purpose of resolving a protein folding pathway that follows protein backbone residues torsional inertia was accomplished.
Results: A new method, torsion angle modeling, was adopted focused on the rotation of dihedral angles. The potential energy was calculated by rotating torsion angles of the peptide with 8 residues. It was found that when moving in the order of torsional inertia, 8 residues swivel in sequence. Six passes were repeated to find the lowest value.
Conclusion: The protein backbone torsion angle plays very important role in predicting protein structure. Actually, it was thousand times faster or more than others to get the obvious pathway.
Keywords
Protein structure simulation; Co-translational folding; Protein backbone; Dihedral angle; Torsion angle; Torsional inertia; Protein folding pathway; TorsAlign; ProtTorter
Protein structure simulation articles; Co-translational folding articles; Protein backbone articles; Dihedral angle articles; Torsion angle articles; Torsional inertia articles; Protein folding pathway articles; TorsAlign articles; ProtTorter articles
Protein structure simulation articles Protein structure simulation Research articles Protein structure simulation review articles Protein structure simulation PubMed articles Protein structure simulation PubMed Central articles Protein structure simulation 2023 articles Protein structure simulation 2024 articles Protein structure simulation Scopus articles Protein structure simulation impact factor journals Protein structure simulation Scopus journals Protein structure simulation PubMed journals Protein structure simulation medical journals Protein structure simulation free journals Protein structure simulation best journals Protein structure simulation top journals Protein structure simulation free medical journals Protein structure simulation famous journals Protein structure simulation Google Scholar indexed journals Co-translational folding articles Co-translational folding Research articles Co-translational folding review articles Co-translational folding PubMed articles Co-translational folding PubMed Central articles Co-translational folding 2023 articles Co-translational folding 2024 articles Co-translational folding Scopus articles Co-translational folding impact factor journals Co-translational folding Scopus journals Co-translational folding PubMed journals Co-translational folding medical journals Co-translational folding free journals Co-translational folding best journals Co-translational folding top journals Co-translational folding free medical journals Co-translational folding famous journals Co-translational folding Google Scholar indexed journals Protein backbone articles Protein backbone Research articles Protein backbone review articles Protein backbone PubMed articles Protein backbone PubMed Central articles Protein backbone 2023 articles Protein backbone 2024 articles Protein backbone Scopus articles Protein backbone impact factor journals Protein backbone Scopus journals Protein backbone PubMed journals Protein backbone medical journals Protein backbone free journals Protein backbone best journals Protein backbone top journals Protein backbone free medical journals Protein backbone famous journals Protein backbone Google Scholar indexed journals Dihedral angle articles Dihedral angle Research articles Dihedral angle review articles Dihedral angle PubMed articles Dihedral angle PubMed Central articles Dihedral angle 2023 articles Dihedral angle 2024 articles Dihedral angle Scopus articles Dihedral angle impact factor journals Dihedral angle Scopus journals Dihedral angle PubMed journals Dihedral angle medical journals Dihedral angle free journals Dihedral angle best journals Dihedral angle top journals Dihedral angle free medical journals Dihedral angle famous journals Dihedral angle Google Scholar indexed journals Torsion angle articles Torsion angle Research articles Torsion angle review articles Torsion angle PubMed articles Torsion angle PubMed Central articles Torsion angle 2023 articles Torsion angle 2024 articles Torsion angle Scopus articles Torsion angle impact factor journals Torsion angle Scopus journals Torsion angle PubMed journals Torsion angle medical journals Torsion angle free journals Torsion angle best journals Torsion angle top journals Torsion angle free medical journals Torsion angle famous journals Torsion angle Google Scholar indexed journals Torsional inertia articles Torsional inertia Research articles Torsional inertia review articles Torsional inertia PubMed articles Torsional inertia PubMed Central articles Torsional inertia 2023 articles Torsional inertia 2024 articles Torsional inertia Scopus articles Torsional inertia impact factor journals Torsional inertia Scopus journals Torsional inertia PubMed journals Torsional inertia medical journals Torsional inertia free journals Torsional inertia best journals Torsional inertia top journals Torsional inertia free medical journals Torsional inertia famous journals Torsional inertia Google Scholar indexed journals Protein folding pathway articles Protein folding pathway Research articles Protein folding pathway review articles Protein folding pathway PubMed articles Protein folding pathway PubMed Central articles Protein folding pathway 2023 articles Protein folding pathway 2024 articles Protein folding pathway Scopus articles Protein folding pathway impact factor journals Protein folding pathway Scopus journals Protein folding pathway PubMed journals Protein folding pathway medical journals Protein folding pathway free journals Protein folding pathway best journals Protein folding pathway top journals Protein folding pathway free medical journals Protein folding pathway famous journals Protein folding pathway Google Scholar indexed journals TorsAlign articles TorsAlign Research articles TorsAlign review articles TorsAlign PubMed articles TorsAlign PubMed Central articles TorsAlign 2023 articles TorsAlign 2024 articles TorsAlign Scopus articles TorsAlign impact factor journals TorsAlign Scopus journals TorsAlign PubMed journals TorsAlign medical journals TorsAlign free journals TorsAlign best journals TorsAlign top journals TorsAlign free medical journals TorsAlign famous journals TorsAlign Google Scholar indexed journals ProtTorter articles ProtTorter Research articles ProtTorter review articles ProtTorter PubMed articles ProtTorter PubMed Central articles ProtTorter 2023 articles ProtTorter 2024 articles ProtTorter Scopus articles ProtTorter impact factor journals ProtTorter Scopus journals ProtTorter PubMed journals ProtTorter medical journals ProtTorter free journals ProtTorter best journals ProtTorter top journals ProtTorter free medical journals ProtTorter famous journals ProtTorter Google Scholar indexed journals
Article Details
Abbreviation:
BLAST: Basic local alignment search tool; DNA: deoxyribonucleic acid; mRNA: messenger ribonucleic acid; NMR: nuclear magnetic resonance; PDB: protein data bank; ProtTorter: protein distorter; RamRMSD: Ramachandran plot root mean square deviation; RNA: ribonucleic acid; SAINT: a sequential algorithm initiated at the nitrogen terminus; TM-align: template modeling-algin; TorsAlign: torsion angle alignment
1. Introduction
Simulation of protein structure has been the most important in bioinformatics. In the methods of prediction, there are homology modeling, threading, and ab initio modeling. Ab initio starts without any results from experiment. So this is more useful than any others to look into the structure of the unknown protein. This constructs it’s structure by physical methods to the bare atoms of the protein. But this involves the defects of inaccuracy and slowness than others in prediction [1]. Developing an algorithm for ab initio modelling to simulate protein structure is very important [2]. This has two types of algorithms; one is molecular dynamics (MD) and the other is Monte Carlo (MC). This randomizes the location of atoms to predict protein structure in 3D space. That sets force fields to estimate atom positions at every moment. Exponential time has spent to calculate all of the unknown protein’s conformations by using the highest capacity computer with MC and MD. Note that the structure of the protein changes between microseconds, and furthermore, the positions of the atoms in this structure occur in shorter pico and femto seconds. Thus, to obtain stable form of the molecule is still difficult for researchers.
In nature protein folds faster and more naturally than this. Namely, in vivo folding is faster than in vitro. So Levinthal addressed paradoxically that there is the apparent pathway in the folding [3]. This is true. And Karplus suggested that the ‘bias towards the native state’ over much of the effective energy surface may govern the folding process [4]. We appreciate this is the pathway of folding that occurs in protein synthesis from mRNA transcript. Computational simulation of this cotranslational folding based on the numerical evidences appeared in 1995 [5-7]. Besides, we introduce many experimental evidences and opinions of researchers for protein folding during intracellular gene translation [8, 9].
It is worth to look into cotranslational folding, because there are differences between simulated and experimental structures. We derived the structures from cotranslational and torsional algorithm. Cotranslational folding simulation was managed before by using SAINT algorithm [7]. 3D molecular dynamics was used in this experiment. All movements in the Cartesian space were considered as possible in most molecular dynamics algorithms by most of the researchers. These employ strong covalent bond stretching and bond angle bending terms in their force fields. Though covalent bond stretching and bond angle bending are affected by the force field, these model’s description abandons the fact that only rotations about covalent single bond occurs. We used, thus, backbone torsion angle as the only degree of freedom to describe the motion of protein folding. These models might hamper to interpret the mechanism of protein folding. And helpful manual modification is restricted from researchers. These difficulties could be settled by torsion angle method. Also this is more realistic than other 3D models full of lattice approximations.
2. Method
The polypeptide is free swivel chain and has levers which collide to water molecules. The collision in the protein folding in the cell follows the Brownian movement. It is much stronger. The calculation of the translational molecular kinetics is based on the translational enthalpy data. Thus, the kinetic energy of the water molecule is,
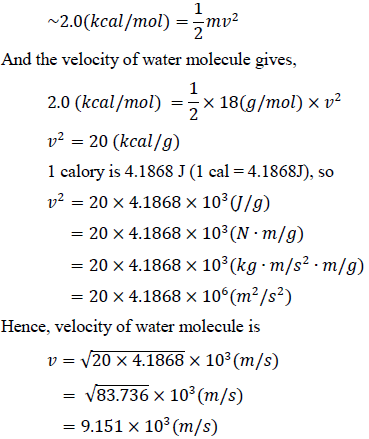
This velocity is fast enough to rotate backbone’s residue with torques [10, 11]. Torsional inertia in the swivels are different for each amino acid. In a backbone, only one residue rotates, the others do not. While the former has small inertia, the latter has larger one. The difference of torsional inertia comes from the type and number of atoms and the length of side chain, and the mass and length of the backbone on both sides of the residue. The middle residue has a small rotational inertia, because the rotational inertia is proportional to the square of the distance. The following (Figure 1) represents only two residues among many in the backbone. Among these connected residues, only two residues with the least rotational inertia were shown. Between them, A has smaller rotational inertia than B. When water molecules collide, A rotates first. B is a residue that stops while residue A rotates, and then returns as soon as A stops.

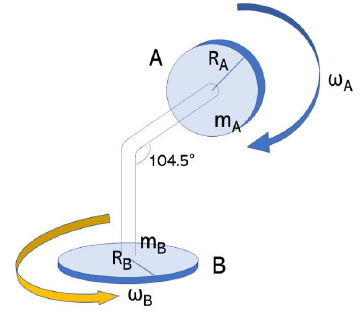
Figure 1: Torque between two residues in a backbone.
If A stops rotation, Pa becomes zero and Pb is not reduced. So B can rotate more easily. If A rotates, Pa becomes larger and Pb is strongly reduced. Therefore, B cannot rotate easily. In Figure 2, the angle between the axel with A residue and B1 is 104.5°. Assuming that B rotates while A also rotates, residue A must handle this rotational movement of residue B. However, if it is 90°, because the radius of rotation (R = 1×R0) is the longest, the rotational inertia of residue B is affected to residue A. Since, residue A can hardly turn without the strongest force because rotational inertia (I = R2×m) is the maximum.
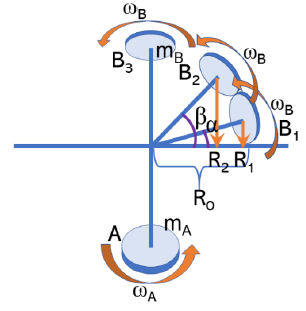
Figure 2: Difference of torque among various bond angles.
To receive the half of the magnitude of the force mentioned above, it must be 135 °. The radius of B2 is,
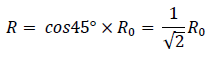
And inertia I is,
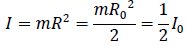
The bond angle between the two residues A and B is 104.5°. The inertia of B2 at 104.5° is,
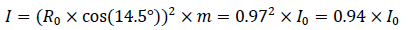
This is almost the same as the value of 90° with the most difficulty. In conclusion, residue B2 cannot rotate with B1 at the same time.
In short, all of the above are summarized as follows. If there are many residues of different sizes, they do not rotate at the same time. The residue with the smallest inertia rotates first. As soon as it stops rotating, the residue with the next smallest inertia turns. When stops rotating, the next residue with more inertia than this rotates. In the case of multiple residues, the rotational inertia is ordered from the smallest.
The coordinates of short polypeptide with important points above was set. And it was compared with the structure from solution NMR. The cotranslational folding and torsional movement of atoms which are different from others was proved. The most representative model of each NMR assay was compared with the structure from the new folding algorithm. Typical structure alignment algorithms, including TM-align [12] were not used in the comparison. These algorithms moves frame with insertions and deletions even in the case of the comparison of identical amino acid sequence. The result of the comparison was represented by logPr and RamRMSD [13]. And it was illustrated in the graph of torsion angle along the residue number (Figure 3). The change of the potential energy during the initial folding and following optimization is also displayed in the graph (Figure 4).
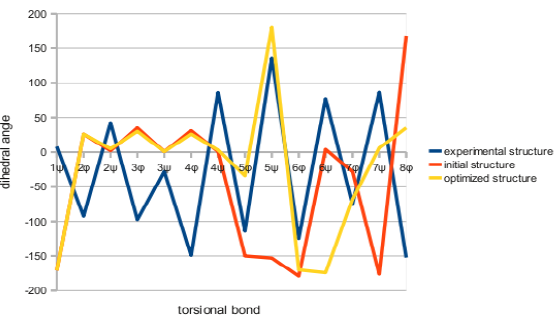
Figure 3: Dihedral angles of Torsional Bonds of Simulated Structures and Experimentally Determined Structure.
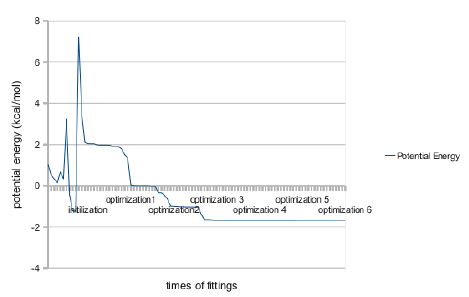
Figure 4: Change of Potential Energy during the Initializations and Optimization.
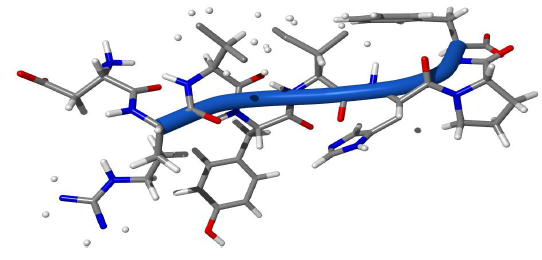
Figure 5: Structure of 1n9v.
2.1 Data set
A single asymmetric chain structure was adopted in the PDB archive on the condition that the length of the chain was 8, the sequence identity was 90% or less, and that there were no heteroatoms. Structures which only contains protein without nucleic acids of DNA, RNA, or DNA-RNA hybrid was selected. Two structures of 1n9v and 1oeh was set. And 1oeh was abandoned because it was fragmented. Finally, 1n9v which is the angiotensin peptide was used in this work. ‘DRVYIHPF’ is the amino acid sequence of 1n9v.
2.2 Cotranslation Folding of Initial Structure
Cotranslational folding was performed with ProtTorter using torsion angles. Whenever a new amino acid was added, the potential energy was calculated, considering every conformation following the change of Φ and ψ angles. As peptide bonds revolve around the backbone, we supposed they move 1 degree by 1 degree. So, 360 cases were observed. Local minima and the global minimum was gotten. These were to predict the initial structure of angiotensin.
2.3 Iterative Optimizations
This simulation became accurate by the peptide collision with water molecules, residues received larger torques, and planar amino acids to rotate faster. The length of the side chain was estimated as the maximum of bonds from the Cα atom. The order of calculation of the pair of bonds of the residue from the sum of the priority from torsional property. The 8 amino acids of 1n9v were arranged into ‘D(7)R(2)V(8)Y(1)I(5)H(4)P(6)F(3)’. The smaller number was calculated first and received higher priority. Consequently, the 4th peptide bond between Tyr (Y) and Ile (I) was first calculated (1+5=6), and the bond between Tyr(Y) and Val(V)(1+8=9). The order of priority is ‘D-(3)-R-(4)-V-(2)-Y-(1)-I-(6)-H-(7)-P-(5)-F’. The numbers in the round brackets designate the order of the linkage among residues. The dihedral angles flanking peptide bond are φ and ψ angles. Between these two dihedral angles, we calculated the one close to the higher priority first, and the other close to the lower priority later. In this order, we iteratively optimized the initial structure from cotranslational folding. This was performed until the convergence of potential energy. The structure in which potential energy converged in six times from the initial structure was taken.
3. Results
Angiotensin was simulated using ProtTorter [14]. While other simulation programs are invisible and untouchable, this can check each structure in every step. This can directly manipulate. Energetically stable local minima structure which is still smaller than the reference structure was observed. The structure of 1n9v from the simulation with ProtTorter is shown in Figure 5. Loop structure was found in most of the 8 residues except the first aspartate residue in the angiotensin peptide. The dihedral angles (Φ, ψ) were usually around the range of (25º-30º, 0º-5º). We can see the vivid difference between this and other simulations (Figure 3). Experimental structure regularly oscillated above and below the 0º, while simulated angles were positive in the N-terminal region. These deviated far from the C-terminal region.
After simulating, we obtained angles and local energy minima. And all of these were arranged into Table 1 for clarity. The initial and six iterations were arrayed in the row of the Table and seven bonds in the column. In the end, 49 arguments were placed in the Table. The ψ angle is written on the top of the cell and the φ in the bottom. In each cell, angles and the number of local minima are written. The structure was simulated from very large search space. As Table 1 shows, initial structure of cotranslational folding was from about 52 conformations. For this peptide composed with 8 residues, the most stable structure was from usually about 70-90 structures. It is very efficient to compare with typical molecular dynamics. LogPr value (Table 2) signifies the difference of the two compared structures with more weight on the more closer similarity. There are eight dihedral angles each for residue from 1 to 8 in both reference and simulated structures. When the two angles of the same residue is very similar, those values were made to be equivalent. On the contrary, they were made to be different.
The logPr values of simulated structures increased toward the later iterations implying the convergence in optimizations. The lowest logPr value of -15.18 was observed from the pair of 5th and 6th optimization. The fact that lower logPr values in the pairs of nearer iterations than the farther ones was found. The highest logPr value among the pairs of adjacent passes was -4.62 in init. and opt. 1 (Table 2). There were difference between the cotranslational path and the torsional one. RamRMSD (Table 2) is the RMS(root mean square) deviation between the positions of residues on the Ramachandran plot [15]. RamRMSD is similar to logPr. This includes the growing similarity among later iterations. Pairs in closer passes had lower RamRMSD values than farther passes. The highest RamRMSD among the pairs of adjacent passes was 47.17. This was calculated from the pair between the initial and the first optimization pass.
|
init. † |
opt. 1‡ |
opt. 2 |
opt. 3 |
opt. 4 |
opt. 5 |
opt. 6 |
|
|
1st bond ang.(min.#) |
|||||||
|
Ψ |
-171(4) |
-171(4) |
-171(4) |
-171(4) |
-171(4) |
-171(4) |
-171(4) |
|
Φ |
26(4) |
27(4) |
26(4) |
26(4) |
26(4) |
26(4) |
26(4) |
|
2nd bond |
|||||||
|
Ψ |
2(2) |
1(5) |
5(5) |
5(5) |
5(5) |
5(5) |
5(5) |
|
Φ |
35(5) |
31(6) |
29(5) |
30(6) |
30(6) |
30(6) |
30(6) |
|
3rd bond |
|||||||
|
Ψ |
1(2) |
0(10) |
2(9) |
1(8) |
1(8) |
1(8) |
1(8) |
|
Φ |
31(4) |
27(9) |
29(9) |
26(8) |
26(8) |
26(8) |
26(8) |
|
4th bond |
|||||||
|
Ψ |
1(2) |
2(6) |
0(8) |
4(8) |
3(7) |
3(7) |
3(9) |
|
Φ |
-150(7) |
-39(10) |
-39(15) |
-35(12) |
-34(11) |
-34(11) |
-34(10) |
|
5th bond |
|||||||
|
Ψ |
-153(12) |
-24(5) |
-1(6) |
-179(11) |
-179(11) |
180(11) |
180(11) |
|
Φ |
-179(8) |
-169(5) |
30(7) |
-166(5) |
-167(11) |
-169(11) |
-170(11) |
|
6th bond |
|||||||
|
Ψ |
4(3) |
-154(8) |
11(6) |
-176(8) |
-175(8) |
-174(8) |
-174(8) |
|
Φ |
-28(4) |
-67(5) |
-41(9) |
-69(5) |
-68(5) |
-68(5) |
-68(5) |
|
7th bond |
|||||||
|
Ψ |
-176(3) |
180(3) |
179(3) |
6(5) |
6(3) |
6(3) |
6(3) |
|
Φ |
168(5) |
168(5) |
171(4) |
34(5) |
35(8) |
35(8) |
35(7) |
|
Search Space |
52 |
72 |
88 |
81 |
86 |
86 |
86 |
† initial structure generated from cotranslational folding with torsional energy calculation; ‡ optimized structure following the folding path determined by the torsional propensity
Table 1: Backbone Dihedral Angle and Number of Energy Minima.
|
init. |
opt. 1 |
opt. 2 |
opt. 3 |
opt. 4 |
opt. 5 |
opt. 6 |
exp. s. |
|
|
init.† |
||||||||
|
logPr |
-16.00 |
-4.62 |
-3.50 |
-4.80 |
-4.84 |
-4.84 |
-4.85 |
-0.80 |
|
RamRMSD |
0.00 |
47.17 |
49.75 |
78.61 |
78.39 |
78.28 |
78.27 |
119.67 |
|
opt. 1‡ |
||||||||
|
logPr |
-16.00 |
-6.75 |
-3.88 |
-3.98 |
-4.84 |
-4.02 |
-0.80 |
|
|
RamRMSD |
0.00 |
29.93 |
61.63 |
61.27 |
61.25 |
61.26 |
134.82 |
|
|
opt. 2 |
||||||||
|
logPr |
-16.00 |
-7.02 |
-5.29 |
-5.25 |
-5.23 |
-1.01 |
||
|
RamRMSD |
0.00 |
45.08 |
45.55 |
45.73 |
45.81 |
116.68 |
||
|
opt. 3 |
||||||||
|
logPr |
-16.00 |
-11.08 |
-10.14 |
-10.13 |
-0.84 |
|||
|
RamRMSD |
0.00 |
0.68 |
1.00 |
1.11 |
135.88 |
|||
|
opt. 4 |
||||||||
|
logPr |
-16.00 |
-13.50 |
-13.47 |
-0.82 |
||||
|
RamRMSD |
0.00 |
0.41 |
0.52 |
136.08 |
||||
|
opt. 5 |
||||||||
|
logPr |
-16.00 |
-15.18 |
-0.82 |
|||||
|
RamRMSD |
0.00 |
0.13 |
136.23 |
|||||
|
opt. 6 |
||||||||
|
logPr |
-16.00 |
-0.82 |
||||||
|
RamRMSD |
0.00 |
136.28 |
||||||
|
exp. s.* |
||||||||
|
logPr |
-16.00 |
|||||||
|
RamRMSD |
0.00 |
|||||||
† initial structure generated from cotranslational torsional folding; ‡ optimized structure following the sequence of folding based on the torsional propensity; * experimentally determined structure
Table 2: Similarity among Structures in Iterations.
In Figure 4, the change of energy in the folding of initial structure and in the optimization were illustrated. The potential energy drastically fluctuated in the simulation of initial structure in cotranslational folding. This partly indicates that addition of amino acid is either favorable or unfavorable in each different circumstance. This fluctuation is different from following iterations. This reflects the strong effect of the change of configurations. During the six passes of optimizations, the potential energy decreased saltatorily. This shows that there are a few critical bonds which strongly influence the potential energy of the whole molecule. Demonstrating the fast convergence of the algorithm to the global energy minima, the potential energy remained as being conserved after three passes of optimizations. Comparing this simulation and others’ experimental structure of 1n9v with RamRMSD and logPr, this is more stable than others by global minimum of –1.704 (kcal/mol). The most correlation between each generated structure from its initial structure with adjacent passes have displayed. This increased for the later rounds of iterations. During the folding simulation, the energy dropped saltatorily (Figure 4). The structure from NMR spectroscopy was very different from this simulation. The average of all logPr values ranged from -0.80 to -1.01. RamRMSD varied from 116.68 to 136.28. Although the simulated structure is somewhat different from the reference experiment, it is quite appreciable regarding the low and negative potential energy of -1.704 (kcal/mol). This negative potential energy remark that this structure is stable in the vacuum environment. This structure is not only a low and stable energy structure, but also a possible actual energy minimum because it is an energy minimum along the torsional propensity path. The torsional propensity path must be the path from Levinthal paradox.
4. Discussion
Results suggest five parts to be discussed as follows. First, the difference of structure was due to the electrostatic interaction of atoms and the torsional barrier of rotatable bonds. Given motive force, a stronger turn is induced. This shortens the length of the loop structure. The structure of α-helix was observed from lattice model without the consideration of any detailed electrostatic or torsional potential energy [16]. Thus, additional restraints of non-electrostatic interaction would induce the current loop structure into well-known helices.
Second, another reason for the difference is the utilized force field. There was difference between NMR spectroscopy and this simulation. It is because that was conducted within an aqueous solution and this was performed under the vacuum environment. The difference between the simulated and the NMR structures was brought by the neglect of the interaction of solvents with the protein molecule. And hydrophobic effect and free energy from solvent accessible surface area could be obtained from experiments. This could be applied to structure simulation.
Third, it is very interesting for its fast convergence of the iterations. Although there is a false convergence, It is quite fast finding converging structure in 6 passes. Converging energy minima were quickly obtained following this method.
Fourth, simplified representation of the three dimensional structure of a protein in torsional system was applied. This regenerates the movements of atoms of polypeptide chain in the cellular environment. The fundamental characters of ribosome bound cotranslational folding could be generated. Three dimensional information can be transformed into one dimension by computing easily. This could be operated with sequence alignment algorithms in personal computer fast and correctly as BLAST [17].
Fifth, ProtTorter adopted torsional representation of atomic movements [14]. The results showed fast convergence to the stable form and which was negative and big in the potential energy. However, this path should be solidly validated referring longer polypeptide chains and larger numbers of test proteins. The structure from this program is different from that of the representative NMR in torsion angle. This occurred in folding pathway or force field.
5. Conclusion
Initial structure formation corresponded cotranslational protein folding. Torsion angels of the residue on backbone rotates one by one following torsional inertia. Optimization based on torsional inertia has reduced the number of candidate structures for the native structure. Stable conformation with low potential energy was obtained after input angiotensin sequence into ProtTorter which has the functions of torsion angle rotations and potential energy calculation. Coordinates of local minima to the stable structure were observed in very short time. The clearest folding pathway was represented in the most stable structure coordinate.
Declarations
Ethics Approval and Consent to Participate
Not applicable.
Consent for Publication
Not applicable.
Availability of Data and Material
Coordinates of the Structure of angiotensin protein is downloadable in PDB archive of RCSB(https://www.rcsb.org) with the index of 1n9v.
Competing Interests
Not applicable.
Funding
Not applicable.
Authors’ Contributions
All of this study was carried out by myself.
Acknowledgements
Not applicable.
References
- Jung S (Seonghoon Jeong old name), Chapter I. Introduction. In: Development of globularity and torsion based analysis methods for protein structures. Seoul National University (2013): 8-19.
- Dill KA, MacCallum JL. The protein-folding problem, 50 years on. Science 338 (2012): 1042-1046.
- Levinthal C. Mössbauer spectroscopy in biological systems proceedings. Univ Illinois Bull 67 (1969): 22-24.
- Karplus M, The levinthal paradox: yesterday and today. Fold Des 2 (1997): 69-75.
- Law E. Computational studies of structural motifs and cotranslational folding mechanisms in membrane and soluble proteins. Oxford University (2017).
- De Oliveira SHP, Shi J, Deane CM. Building a better fragment library for de novo protein structure prediction. PLoS One 10 (2015): e0123998.
- Ellis JJ, Huard FPE, Deane CM, et al. Directionality in protein fold prediction. BMC Bioinformatics 11 (2010): 172.
- Cymer F, von Heijne G. Cotranslational folding of membrane proteins probed by arrest-peptide-mediated force measurements. Proc Natl Acad Sci USA 110 (2013): 14640-14645.
- Fedorov AN, Baldwin TO. Co-translational protein folding. J Biol Chem 272 (1997): 32715-32718.
- Serway RA, Jewett Jr JW. Chapter 10. Rotation of a rigid object about a fixed axis. In: Physics for scientists and engineers. 10th Brooks Cole (2003): 292-335.
- Stillinger FH. Theory and molecular models for water. In Eds.: Prigogine I, Rice SA. Advances in chemical physics, volume XXXI, John Wiley & Sons (1975): 68.
- Zhang Y, Skolnick J. TM-align: A protein structure alignment algorithm based on the TM-score. Nucl Acids Res 33 (2005): 2302-2309.
- Jung S, Bae S, Son HS. Validity of protein structure alignment method based on backbone torsion angles. J Proteom Bioinform 4 (2011): 10.
- Jung S (Seonghoon Jeong old name), Chapter V. ProtTorter: A protein structure modeler with torsion angle system. In: Development of globularity and torsion based analysis methods for protein structures. Seoul National University (2013): 86-113.
- Ramakrishnan C, Ramachandran GN. Stereochemical criteria for polypeptide and protein chain conformations, II. Allowed conformations for a pair of peptide units. Biophys J 5 (1965): 909-933.
- Leach AR. Molecular modeling: principles and applications. 2nd Prentice Hall (2001): 513, 516, 519.
- Altschul SF, Gish W, Miller W, et al. Basic local alignment search tool. J Mol Biol 215 (1990): 403-410.


 Impact Factor: * 4.2
Impact Factor: * 4.2 CiteScore: 2.9
CiteScore: 2.9  Acceptance Rate: 11.01%
Acceptance Rate: 11.01%  Time to first decision: 10.4 days
Time to first decision: 10.4 days  Time from article received to acceptance: 2-3 weeks
Time from article received to acceptance: 2-3 weeks 